Формула метанола СН3-ОН. Молекулярная формула метанола СН4О. Уравнение реакции горения метанола:
Вычислим массу метанола:
Вычислим молярную массу метанола:
Вычислим количество вещества метанола:
По уравнению реакции для сгорания 2 моль метанола необходимо 3 моль кислорода. Пусть для сжигания 25 моль метанола нужно х моль кислорода. Составим пропорцию:
Вычислим объем кислорода:
В воздухе содержится около 21% кислорода, или 0,21. Вычислим объем воздуха, необходимый для сжигания метанола:
1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.
Найдём координаты точки Н - середины ДИАГОНАЛИ АС:
Итак, Н(7,7,1) .
Вычислим высоту МН пирамиды:
2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:
Итак, Р(3,4,1) . Следовательно,
3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:
Формула метанола СН3-ОН. Молекулярная формула метанола СН4О. Уравнение реакции горения метанола:
Вычислим массу метанола:
Вычислим молярную массу метанола:
Вычислим количество вещества метанола:
По уравнению реакции для сгорания 2 моль метанола необходимо 3 моль кислорода. Пусть для сжигания 25 моль метанола нужно х моль кислорода. Составим пропорцию:
Вычислим объем кислорода:
В воздухе содержится около 21% кислорода, или 0,21. Вычислим объем воздуха, необходимый для сжигания метанола:
ответ: необходимо 4 м3 воздуха.
1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.
Найдём координаты точки Н - середины ДИАГОНАЛИ АС:
Итак, Н(7,7,1) .
Вычислим высоту МН пирамиды:
2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:
Итак, Р(3,4,1) . Следовательно,
3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:
ВЫЧИСЛИМ ПЕРИМЕТР ПИРАМИДЫ: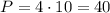 .
.
Вычислим площадь боковой поверхности пирамиды: