Два перпендикулярных отрезка km и ln пересекаются в общей серединной точке p.
какой величины∡ n и ∡ k, если ∡ l = 20° и ∡ m = 70°?
1. отрезки делятся пополам, значит, kp =
,
= lp,
∡
= ∡ mpl, так как прямые перпендикулярны и оба угла равны
°.
по первому признаку равенства треугольник kpn равен треугольнику mpl.
2. в равных треугольниках соответствующие углы равны.
в этих треугольниках соответствующие ∡
и ∡ m, ∡
и∡ l.
∡ k =
°;
∡ n =
°.
1. 74
2. 136
3. 60
Объяснение:
1. окружность составляет 360 градусов, значит дуга АС = 360 - 140 - 72 = 148.
угол АВС опирается на дугу АС, значит равен половине этой дуги = 148:2 =74
2. Дуга АС равна угол АВС *2 = 22*2 = 44
т.к угол АОС опирается на диаметр, то он равен 44.
Угол АОС и АОВ смежные, в сумме 180 градусов, значит АОВ = 180 - 44 = 136
3. Угол ДВС опирается на дугу ДС, значит дуга ДС = 30*2 = 60
Угол ДОС опирается на диаметр, значит равен 60
АОВ и ДОС равны (вертикальные углы равны), следовательно, стягивают равные дуги. Т.е дуга АВ = 60
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
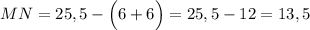 (см)
(см)
ответ: