Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P и образуют два равных треугольника KPN и MPL. Расстояние между точками K и L равно 28 см. Какое расстояние между точками M и N? 1. У равных треугольников все соответственные элементы равны, стороны KP=... и NP = ... как соответственные стороны равных треугольников.
∡К = ...° и ∡ =... °, так как смежные с ними углы ∡ KPN = ∡ MPL = ...°. По первому признаку треугольник KPL равен треугольнику ... 2. В равных треугольниках соответственные стороны равны. Для стороны KL соответственная сторона — MN. MN = ... см.
1) Как называется утверждение которое нельзя доказать?
Аксиома.
2) Из теоремы "Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны" составьте обратную.
Меняем "если" и "то" местами: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Как называются прямые на плоскости, не имеющие общих точек?
Параллельными.
4) Если прямая a параллельна прямой b, и прямая а параллельна прямой с, то что можно сказать о прямых b и c?
Тогда b║c.
5) Изобразите: две параллельные прямые пересеченные секущей, отметьте числами 5 и 6 углы, которые являются односторонними.
См. рисунок.
6) О равенстве каких углов можно утверждать, если параллельные прямые пересечены секущей.
Тогда равны накрест лежащие углы: ∠1 = ∠7, ∠4 = ∠6
и равны соответственные углы: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8.
1.
∆АВС≈∆AMK по 3-ём углам (∠А-общий, ∠AMK=∠ABC как соответственные при секущей AB и MK║BC, ∠AKM=∠ACB как соответственные при секущей AC и MK║BC) ⇒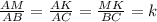
AM/AB=4/6=MK/BC=8/x x=6·8:4=12 см - BC
AM/AB=4/6=AK/AC=9/y y=6·9:4=13,5 см - AC
ответ: 12 см - BC и 13,5 см - AC
2.
По свойству медиан в треугольнике:
BO=8=2x ⇒ OK=x=4 см
AD=3х=24 ⇒ OD=x=8 см, а AO=2x=16 см
ответ: ОК=4; АО=16; ОD=8
3.
ВD - биссектриса ∆АВС ⇒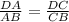
Пусть DA=x, тогда DC = 11-x
Составим пропорцию: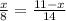
14x=88-8x
14x+8x=88
22x=88
x=4 см - сторона AD
11-4=7 cм- сторона DC
ответ: 4 см - сторона AD и 7 cм- сторона DC