Дуга AB = 49 градусов дуга BC = 11 градусов значит дуга CB = 60 градусов, но это минимальная из двух дуг, а если рассматривать душу в круге, которая большая, то душа CB = 360 - 60 градусов, значит угол, образуемый большей дугой CB, в вершине A - искомый и внутренний, значит равен половине дуги, опирающиеся на окружность, значит угол САВ = (360 - 60)/2 = 150 градусов
Чёт фигово решаю, задачу, она вообще по другому решается. Дуга СА - и угол АBC - связаны, так, что Угол ABC опирается на дугу CA = 11. Значит Угол ABC- внутренний, и равен половине дуги в градусах, на которую он опирается, значит ABC = 11/2 = 5.5
У произвольного треугольника есть формула площади :
, где h - высота, а - сторона, на которое падает основание высоты.
Прямоугольный же треугольник является частным случаем треугольника с тем отличием, что один из его углов равен 90 градусов. Тем не менее это не отменяет того факта, что для него работают все те же самые формулы, что и для обычного треугольника, поэтому площадь прямоугольного треугольника можно найти по нескольким формулам :
1. , где a и b - катеты (так как они пересекаются под углом в 90 градусов одного из них можно считать высотой)
2. , где c - гипотенуза, h - высота, опущенная на гипотенузу как на одно из оснований треугольника
дуга BC = 11 градусов
значит дуга CB = 60 градусов, но это минимальная из двух дуг, а если рассматривать душу в круге, которая большая, то душа CB = 360 - 60 градусов, значит угол, образуемый большей дугой CB, в вершине A - искомый и внутренний, значит равен половине дуги, опирающиеся на окружность,
значит угол САВ = (360 - 60)/2 = 150 градусов
Чёт фигово решаю, задачу, она вообще по другому решается. Дуга СА - и угол АBC - связаны, так, что Угол ABC опирается на дугу CA = 11. Значит Угол ABC- внутренний, и равен половине дуги в градусах, на которую он опирается, значит ABC = 11/2 = 5.5
У произвольного треугольника есть формула площади :
Прямоугольный же треугольник является частным случаем треугольника с тем отличием, что один из его углов равен 90 градусов. Тем не менее это не отменяет того факта, что для него работают все те же самые формулы, что и для обычного треугольника, поэтому площадь прямоугольного треугольника можно найти по нескольким формулам :
1.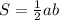 , где a и b - катеты (так как они пересекаются под углом в 90 градусов одного из них можно считать высотой)
, где a и b - катеты (так как они пересекаются под углом в 90 градусов одного из них можно считать высотой)
2.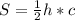 , где c - гипотенуза, h - высота, опущенная на гипотенузу как на одно из оснований треугольника
, где c - гипотенуза, h - высота, опущенная на гипотенузу как на одно из оснований треугольника