Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
Где угол лежит напротив стороны , угол лежит напротив стороны , а угол лежит напротив стороны , а - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что
Но тогда теорему синусов можно переписать так:
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок. (нижние углы), то есть треугольник равнобедренный с основанием , значит, боковые стороны равны, то есть
Далее, , то треугольник равнобедренный с основанием , боковые стороны равны, то есть
ответ:по правилу сумма всех углов треугольника равен 180°
Объяснение:у треугольника 3 угла если все 180° то каждые 60°
Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
Где угол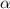 лежит напротив стороны
лежит напротив стороны  , угол
, угол 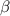 лежит напротив стороны
лежит напротив стороны 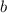 , а угол
, а угол 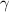 лежит напротив стороны
лежит напротив стороны  , а
, а 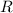 - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
- радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что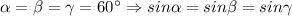
Но тогда теорему синусов можно переписать так:
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок.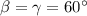 (нижние углы), то есть треугольник равнобедренный с основанием
(нижние углы), то есть треугольник равнобедренный с основанием  , значит, боковые стороны равны, то есть
, значит, боковые стороны равны, то есть 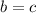
Далее,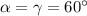 , то треугольник равнобедренный с основанием
, то треугольник равнобедренный с основанием 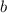 , боковые стороны равны, то есть
, боковые стороны равны, то есть 
Ну и завершающий вывод:
Что и требовалось доказать.