Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда \angle BAL= \angle CAL как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса \angle BAC. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой \angle BAC. Заметим, что \angle BCL= \angle CBL как вписанные углы, опирающиеся на равные дуги.
Пусть \angle BCL= x. Четырехугольник ACLB — вписанный, поэтому \angle ACL плюс \angle ABL = 180 в степени circ, то есть 40 в степени circ плюс x плюс 90 в степени circ плюс x = 180 в степени circ , откуда x = 25 в степени circ. Так как точки K и L совпадают, \angle BCK = \angle BCL = 25 в степени circ.
1.
Расстояние между точкой A & прямой a — проекция наклонной Ba, или просто — катет.
Другого определения здесь невозможно дать, этот треугольник обязательно должен быть прямоугольным.
<B = 30°; Теоерема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Напротив угла <B — лежит катет Aa, тоесть: Aa = Ba/2.
Катет Aa — мы можем найти только теоремой Пифагора:
Вывод: Aa = 2.31.
2.
<A = 90°; <B == <C => BA == AC.
BC (гипотенуза) = 14; по теореме Пифагора:
Нарисуем дополнительную высоту, проведённую через прямой угол: Высота AM.
В равнобедренном прямоугольном треугольнике — высота, проведённая к гипотенузе — это — и медиана, и высота, и биссектриса.
То есть: AM == MC = 14/2 (свойство медианы в прямоугольном треугольнике) = 7.
Вывод: AM = 7.
3.
<B = 30° => AC = BC/2 (теорема о 30-градусном угле).
Опять же, теорема Пифагора:
Высоту нарисуем дополнительную, в рисунке — её нет.
Добавим новую точку на гипотенузе BC — пусть будет — M.
Отрезок AM — это и есть расстояние между прямой a — и точкой A.
<MAC = 90 - <C = 90-60 = 30° => MC = AC/2 (теорема о 30-градусном угле).
MC = AC/2 => MC = 11.54/2 = 5.8.
По теореме Пифагора:
Вывод: MC = 9.99.
\\ВНИМАНИЕ!
Теорема Пифагора такова: Сумма квадратов катетов равна квадрату гипотенузы, тоесть: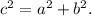 \\
\\
Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда \angle BAL= \angle CAL как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса \angle BAC. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой \angle BAC. Заметим, что \angle BCL= \angle CBL как вписанные углы, опирающиеся на равные дуги.
Пусть \angle BCL= x. Четырехугольник ACLB — вписанный, поэтому \angle ACL плюс \angle ABL = 180 в степени circ, то есть 40 в степени circ плюс x плюс 90 в степени circ плюс x = 180 в степени circ , откуда x = 25 в степени circ. Так как точки K и L совпадают, \angle BCK = \angle BCL = 25 в степени circ.
ответ: 25°.
Раздел кодификатора ФИПИ: Углы в окружностях