Расстояние от точки K до прямой MN - отрезок FK, равный (см).
Объяснение:
1. Рассмотрим равносторонний ΔMNK:
Т.к. ΔMNK - равносторонний, то каждый угол будет равняться .
По условию из точки K к отрезку MN проведём биссектрису KF, которая по свойству делит ∠K на два равных угла.
⇒ ∠NKF = ∠FKM = 60° : 2 = 30°.
Расстояние от точки до прямой/отрезка - перпендикуляр.
⇒ Проводим из вершины F перпендикуляр к отрезку MK, равный (см).
Благодаря этому перпендикуляру, получаем прямоугольный ΔFGK с прямым углом G (оставшиеся два угла - острые).
2. Рассмотрим прямоугольный ΔFGK:
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет FG в 2 раза меньше гипотенузы FK, т.е. FK = (см).
Т.к. ΔMNK - равносторонний ⇒ он является и равнобедренным с основанием NM.
Биссектриса, проведённая к основанию равнобедренного треугольника, является и высотой, и медианой.
⇒ биссектриса FK - высота треугольника MNK, и в тоже время перпендикуляр к прямой MN.
⇒ отрезок FK - расстояние от точки K до прямой MN.
ответ: A) 2:9
Так как у горизонтальных прямоугольников равны длинные стороны и равны площади, то и короткие стороны равны.
Обозначим их х. Тогда АВ = 3х, AD = 2AB = 6x.
Сторона 4-го прямоугольника - у (см. рис.)
Итак, стороны закрашенного прямоугольника равны х и (6х - у).
Так как S₂ = S₄, составим уравнение:
(6x - y) · x = 3x · y
6x² - xy = 3xy
6x² = 4xy
Так как х ≠ 0, разделим обе части на 2х:
3x = 2y
y = 3/2 x = 1,5х
Вторая сторона закрашенного прямоугольника:
6x - y = 6x - 1,5x = 4,5x
Тогда отношение его сторон:
x : (4,5x) = 1 : (9/2) = 2 : 9
Расстояние от точки K до прямой MN - отрезок FK, равный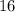 (см).
(см).
Объяснение:
1. Рассмотрим равносторонний ΔMNK:
Т.к. ΔMNK - равносторонний, то каждый угол будет равняться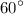 .
.
По условию из точки K к отрезку MN проведём биссектрису KF, которая по свойству делит ∠K на два равных угла.
⇒ ∠NKF = ∠FKM = 60° : 2 = 30°.
Расстояние от точки до прямой/отрезка - перпендикуляр.
⇒ Проводим из вершины F перпендикуляр к отрезку MK, равный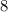 (см).
(см).
Благодаря этому перпендикуляру, получаем прямоугольный ΔFGK с прямым углом G (оставшиеся два угла - острые).
2. Рассмотрим прямоугольный ΔFGK:
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет FG в 2 раза меньше гипотенузы FK, т.е. FK =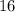 (см).
(см).
Т.к. ΔMNK - равносторонний ⇒ он является и равнобедренным с основанием NM.
Биссектриса, проведённая к основанию равнобедренного треугольника, является и высотой, и медианой.
⇒ биссектриса FK - высота треугольника MNK, и в тоже время перпендикуляр к прямой MN.
⇒ отрезок FK - расстояние от точки K до прямой MN.
ответ: A) 2:9
Объяснение:
Так как у горизонтальных прямоугольников равны длинные стороны и равны площади, то и короткие стороны равны.
Обозначим их х. Тогда АВ = 3х, AD = 2AB = 6x.
Сторона 4-го прямоугольника - у (см. рис.)
Итак, стороны закрашенного прямоугольника равны х и (6х - у).
Так как S₂ = S₄, составим уравнение:
(6x - y) · x = 3x · y
6x² - xy = 3xy
6x² = 4xy
Так как х ≠ 0, разделим обе части на 2х:
3x = 2y
y = 3/2 x = 1,5х
Вторая сторона закрашенного прямоугольника:
6x - y = 6x - 1,5x = 4,5x
Тогда отношение его сторон:
x : (4,5x) = 1 : (9/2) = 2 : 9