Исследование Постройте произвольный треугольник; Проведите две медианы из любых двух вершин треугольника. Точку пересечения медиан обозначьте О. Возьмите линейку и измерьте расстояние от вершины треугольника до точки О. Запишите ответ……….. От точки О до середины противоположной стороны (точка образованная данной медианой). Запишите ответ……………… Во сколько раз расстояние от вершины треугольника до точки О больше расстояния от точки О до середины противоположной стороны? ответ:……………………………… Запишите результат в виде отношения…………………. Сформулируйте вывод: Медианы треугольника пересекаются в ………. точке, которая делит каждую медиану в отношении………., считая от вершины.
ВО = ДО = 5 см
АМ = СМ = √(9²+12²) =√(81+144) = √225 = 15 см
МС = МД = √(5²+12²) =√(25+144) = √169 = 13 см
Расстояния между основаниями? Это как? Стороны и диагонали ромба?
AB = BC = СД = АД = √(9²+5²) =√(81+25) = √106 см
АС и ВД даны по условию.
---
2 варианта, к сожалению!
1) АС - гипотенуза
AO = AC/2 = 7,5 см
О - центр описанной окружности треугольника АВС и поэтому
АК = ВК = СК = √(7,5² + 8,5²) = √(15² + 17²)/2 = √(225+289)/2 = √514/2 см
2) AB - гипотенуза
АВ = √(8² + 15²) = √(64+225) = √289 = 17 см
AO = AВ/2 = 8,5 см
АК = ВК = СК = √(8,5² + 8,5²) = 8,5√2 см
1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.
Найдём координаты точки Н - середины ДИАГОНАЛИ АС:
Итак, Н(7,7,1) .
Вычислим высоту МН пирамиды:
2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:
Итак, Р(3,4,1) . Следовательно,
3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:
ВЫЧИСЛИМ ПЕРИМЕТР ПИРАМИДЫ: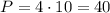 .
.
Вычислим площадь боковой поверхности пирамиды: