1) дано угол В=30 градусов ВА=4 см
решение
проведем АС перпендикуляр к прямой а угол ВСА=90 градусов
получим прямоугольный треугольник АВС
пусть АС=х тогда по свойству что против угла в 30 градусов лежит катет равный половине гипотинузы х=ВА\2
значит АС= 2 см ответ 2 см
2) дано: треугольник АВС равнобедренный (так как угли при основании равны) ВС=14см
проведем АР
т.к. АВС равнобедренный то АР высота медиана биссектриса
значит ВР=СР=14\2=7см
треугольник арс прямоугольный и равнобедренный т.к. угол рас =180-90-45=45 градусов
значит ар=7см
3) тут не дано ни одной величины
это треугольник прямоугольный т.к. 180-30-60=90
значит катет лежащий против угла в 30 градсов равен половине гипотинузы следовательно ас=х тогда вс=2х
тогда ва^2=4х^2-x^2
ва=х
если провести высоты ар то получим новый прямоугольный треугольник вра в котором ар=(х)\2
Объяснение:
1) Цилиндр описанный, => прямоуг.треуг.вписан в окружность, => R равен половине гипотенузы
треугольник равнобедренный, по т.Пифагора
(2R)^2 = 2x^2, где x---катет
R^2 = x^2 / 2
R = x / корень(2)
Sбок.призмы = высота * (x+x+гипотенуза) = 40
2x + 2R = 40/10 = 4
x+R = 2
x = 2-R
R = (2-R) / корень(2)
2-R-Rкорень(2) = 0
2-R(1+корень(2)) = 0
R = 2 / (1+корень(2))
можно избавиться от иррациональности в знаменателе:
домножить числитель и знаменатель на сопряженное выражение (1-корень(2))
R = 2(1-V2) / ((1-V2)(1+V2)) = 2(1-V2) / (1-2) = 2(корень(2) - 1)
2) tgα=h/R, где R-радиус основания конуса, h-высота конуса
Следовательно, h=R*tgα
2)S(сеч)=ah/2=(2Rh)/2=Rh
S(сеч)=Q => Rh=Q =>R*R*tgα=Q
R²tgα=Q
R=√(Q/tgα)
3)L=2ПR
L=2П√(Q/tgα)
3) 24 ( фото с объяснением сверху)
4) Vшара=4пR^3/3
288п=4пR^3/3
R=6
Hцилиндра=2R=12
Sполповцил=2пR(R+H)=216п
1) дано угол В=30 градусов ВА=4 см
решение
проведем АС перпендикуляр к прямой а угол ВСА=90 градусов
получим прямоугольный треугольник АВС
пусть АС=х тогда по свойству что против угла в 30 градусов лежит катет равный половине гипотинузы х=ВА\2
значит АС= 2 см ответ 2 см
2) дано: треугольник АВС равнобедренный (так как угли при основании равны) ВС=14см
проведем АР
т.к. АВС равнобедренный то АР высота медиана биссектриса
значит ВР=СР=14\2=7см
треугольник арс прямоугольный и равнобедренный т.к. угол рас =180-90-45=45 градусов
значит ар=7см
3) тут не дано ни одной величины
это треугольник прямоугольный т.к. 180-30-60=90
значит катет лежащий против угла в 30 градсов равен половине гипотинузы следовательно ас=х тогда вс=2х
тогда ва^2=4х^2-x^2
ва=х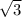
если провести высоты ар то получим новый прямоугольный треугольник вра в котором ар=(х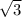 )\2
)\2
Объяснение:
1) Цилиндр описанный, => прямоуг.треуг.вписан в окружность, => R равен половине гипотенузы
треугольник равнобедренный, по т.Пифагора
(2R)^2 = 2x^2, где x---катет
R^2 = x^2 / 2
R = x / корень(2)
Sбок.призмы = высота * (x+x+гипотенуза) = 40
2x + 2R = 40/10 = 4
x+R = 2
x = 2-R
R = (2-R) / корень(2)
2-R-Rкорень(2) = 0
2-R(1+корень(2)) = 0
R = 2 / (1+корень(2))
можно избавиться от иррациональности в знаменателе:
домножить числитель и знаменатель на сопряженное выражение (1-корень(2))
R = 2(1-V2) / ((1-V2)(1+V2)) = 2(1-V2) / (1-2) = 2(корень(2) - 1)
2) tgα=h/R, где R-радиус основания конуса, h-высота конуса
Следовательно, h=R*tgα
2)S(сеч)=ah/2=(2Rh)/2=Rh
S(сеч)=Q => Rh=Q =>R*R*tgα=Q
R²tgα=Q
R=√(Q/tgα)
3)L=2ПR
L=2П√(Q/tgα)
3) 24 ( фото с объяснением сверху)
4) Vшара=4пR^3/3
288п=4пR^3/3
R=6
Hцилиндра=2R=12
Sполповцил=2пR(R+H)=216п