Пусть сторона равностороннего треугольника = a.
Так как треугольник равносторонний, то медиана в нем будет являться еще биссектрисой и высотой.
Тогда по т. Пифагора имеем:
a²=(9√3)²+()²
a²=243+
4a²=243*4+a²
3a²=972
a²=324
a=±18 (-18 не учитываем, так как это сторона, а она не может быть отрицательна, ну ты понял))
ответ: 18
равносторонний треугольник АВС,
ВЕ — медиана,
ВЕ = 9 √3.
Найти сторону треугольника АВ — ?
Решение:
Рассмотрим равносторонний треугольник АВС. Медиана ВЕ является высотой. Рассмотрим прямоугольный треугольник АЕС. Пусть АВ = х сантиметров. тогда АЕ = х/2. По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов):
АЕ^2 + ВЕ^2 = АВ^2:
х^2/4 + (9√3)^2 = х^2;
х^2/4 + 243 = х^2;
х^2 + 972 = 4х^2;
4х^2 - х^2 = 972;
3 х^2 = 972;
х^2 = 972 : 3;
х^2 = 324;
х = 18 сантиметров.
ответ :18 см
Пусть сторона равностороннего треугольника = a.
Так как треугольник равносторонний, то медиана в нем будет являться еще биссектрисой и высотой.
Тогда по т. Пифагора имеем:
a²=(9√3)²+(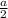 )²
)²
a²=243+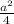
4a²=243*4+a²
3a²=972
a²=324
a=±18 (-18 не учитываем, так как это сторона, а она не может быть отрицательна, ну ты понял))
ответ: 18