На топографической карте (рис. 7) по километровой сетке най- дите точку высоты на уровнем моря 145.0 (кетка 13—56) и праксу 1530 (клетка 12-54) и определите расстояние между ними
Шар можно описать около призмы, если она прямая и ее основания являются многоугольниками, вписанными в окружность. Центр шара лежит на середине высоты призмы, соединяющий центры окружностей, описанных около основания призмы.
Полуплоскость ограничена прямой, параллельной боковому ребру призмы и проходящей через центр шара.
— радиус шара; диагональ призмы
Поскольку призма правильная, то в основе лежит квадрат, тогда диагональ АС: см
По теореме Пифагора из прямоугольного треугольника , найдем высоту призмы.
Под корнем отрицательное число, что-то в условии не так
Отрезок АВ, середина его - точка С, Расстояние от точки А до прямой м Д = 15см. Проецируем точки А, В, С на прямую Л, получаем точки а, в, с. конец А удалён от прямой Л на Аа =9 см, конец В - на Вв = 5 см. Все эти точки расположены на одинаковом расстоянии от прямой м. Обозначим это расстояние д. найдём д из теоремы Пифагора д² = 15² - Аа² = 225 - 81 = 144 ---> д = 12 Расстояние от точки В до прямой м равно √(д² + Вв²) = √(144 + 25) = √169 = 13 Точка С (середина отрезка АВ) удалена от прямой Л на Сс = 0,5(Аа + Вв) = 0,5 (9 + 5) = 7 Расстояние от точки С до прямой м равно √(д² + СС²) = √(144 + 49) = √193
Шар можно описать около призмы, если она прямая и ее основания являются многоугольниками, вписанными в окружность. Центр шара лежит на середине высоты призмы, соединяющий центры окружностей, описанных около основания призмы.
Полуплоскость ограничена прямой, параллельной боковому ребру призмы и проходящей через центр шара.
Поскольку призма правильная, то в основе лежит квадрат, тогда диагональ АС: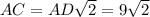 см
см
По теореме Пифагора из прямоугольного треугольника , найдем высоту призмы.
, найдем высоту призмы.
Под корнем отрицательное число, что-то в условии не так
Расстояние от точки А до прямой м Д = 15см.
Проецируем точки А, В, С на прямую Л, получаем точки а, в, с.
конец А удалён от прямой Л на Аа =9 см, конец В - на Вв = 5 см.
Все эти точки расположены на одинаковом расстоянии от прямой м. Обозначим это расстояние д.
найдём д из теоремы Пифагора д² = 15² - Аа² = 225 - 81 = 144 ---> д = 12
Расстояние от точки В до прямой м равно √(д² + Вв²) = √(144 + 25) = √169 = 13
Точка С (середина отрезка АВ) удалена от прямой Л на
Сс = 0,5(Аа + Вв) = 0,5 (9 + 5) = 7
Расстояние от точки С до прямой м равно √(д² + СС²) = √(144 + 49) = √193