Больший угол ромба равен 120°.
Объяснение:
Диагонали ромба равны а и а√3. Найдите больший угол ромба.
Дано: ABCD - ромб;
АС и BD - диагонали;
AC = a; BD = a√3.
Найти: ∠А.
Рассмотрим ΔАВО.
⇒ ΔАВО - прямоугольный.
⇒
⇒ ∠BAO = arctg (√3) = 60°
⇒ ∠ВАО = ∠OAD = 60°
Тогда ∠А = ∠ВАО + ∠OAD = 120°
В условии ошибка: ВС ║AD, а не АС, так как параллельные прямые не могут проходить через одну точку.
BF = DE по условию,
∠AED = ∠CFB по условию,
∠CBF = ∠ADE как накрест лежащие при пересечении параллельных прямых ВС и AD секущей BD, ⇒
ΔCBF = ΔADE по стороне и двум прилежащим к ней углам.
Значит CF = AE,
BE = BF - EF, DF = DE - EF, а так как BF = DE, то и BE = DF,
∠CFD = ∠AEB как смежные с равными углами (∠AED = ∠CFB по условию),
значит ΔCFD = ΔAEB по двум сторонам и углу между ними.
Тогда ∠АВЕ = ∠CDF, а эти углы - накрест лежащие при пересечении прямых АВ и CD секущей BD, значит АВ║CD.
Больший угол ромба равен 120°.
Объяснение:
Диагонали ромба равны а и а√3. Найдите больший угол ромба.
Дано: ABCD - ромб;
АС и BD - диагонали;
AC = a; BD = a√3.
Найти: ∠А.
Рассмотрим ΔАВО.
Диагонали ромба взаимно перпендикулярны.⇒ ΔАВО - прямоугольный.
Диагонали ромба точкой пересечения делятся пополам.⇒
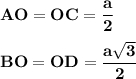
Тангенс угла - отношение противолежащего катета к прилежащему.⇒ ∠BAO = arctg (√3) = 60°
Диагонали ромба являются биссектрисами его углов.⇒ ∠ВАО = ∠OAD = 60°
Тогда ∠А = ∠ВАО + ∠OAD = 120°
Больший угол ромба равен 120°.
В условии ошибка: ВС ║AD, а не АС, так как параллельные прямые не могут проходить через одну точку.
BF = DE по условию,
∠AED = ∠CFB по условию,
∠CBF = ∠ADE как накрест лежащие при пересечении параллельных прямых ВС и AD секущей BD, ⇒
ΔCBF = ΔADE по стороне и двум прилежащим к ней углам.
Значит CF = AE,
BE = BF - EF, DF = DE - EF, а так как BF = DE, то и BE = DF,
∠CFD = ∠AEB как смежные с равными углами (∠AED = ∠CFB по условию),
значит ΔCFD = ΔAEB по двум сторонам и углу между ними.
Тогда ∠АВЕ = ∠CDF, а эти углы - накрест лежащие при пересечении прямых АВ и CD секущей BD, значит АВ║CD.