Найдите координаты точки пересечения плоскости, проходящей через точки A=(-4;-4;1), B=(-6;0;3), C=(-6;-2;2) c прямой, проходящей через точки D=(11;-23;-11), E=(-22;10;11).

ответ: Из точки К на основания двух противоположных боковых граней опустим апофемы КН и КН1. Угол НКН1 = 90 градусов (так как грани перпендикулярны и КН ⊥ AD,  КН1 ⊥ BC). Из условия задачи следует, что НН1 = 6√2. Рассмотрим ΔНКН1 - прямоугольный. В нем КН=КН1=НН1/√2=6√2/√2=6. Теперь рассмотрим ΔОКН - тоже прямоугольный, тк КО - высота пирамиды. ОН=1/2 * НН1= 6√2/2=3√2.

По теореме Пифагора: КО² = КН² - ОН² = 6²-18 = 18 ⇒ КО = 3√2.

АС - диагональ квадрата ABCD, она равна DC*√2 = 6√2*√2 = 12.

Площадь ΔКАС(площадь диагонального сечения) = 1/2 * КО * АС =

= 1/2 * 3√2 * 12 = 18√2

ответ: 2

Объяснение:

, где

Sп.п - площадь полной поверхности

Sосн. - площадь основания

Sбок - площадь боковой грани

Рассмотрим основание призмы

Мы можем узнать сторону основания(понадобиться позже). Тк. по свойству ромба его диагонали перпендикулярны и делятся пополам, то ромб разбит на 4 равных прямоугольных треугольника с катетами 5 и 12. Рассмотрим 1 из них.

По т. Пифагора:

Площадь ромба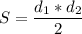

Подставляем в формулу площади полной поверхности призмы

Мы знаем, что боковая грань - прямоугольник,т.е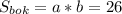  

Т.к. нам известна одна из сторон(сторона основания, которая равна 13), то мы можем найти и боковое ребро