Найдите координаты точки симметричной точке А (6; -8): а) относительно начала координат; б) относительно оси Ох; в) относительно оси Оу; г) относительно прямой у = х; д) относительно прямой у = -х.
3) Диагональ квадрата равна произведению его стороны на , тогда:
ответ: .
4) По теореме Пифагора:
.
Площадь прямоугольного треугольника равна полупроизведению его катетов.
.
ответ: 6; 24.
5) Треугольник равнобедренный (по условию). В равнобедренном треугольнике высота является биссектрисой и медианой. Образовавшиеся два треугольника являются прямоугольными. По теореме Пифагора:
ответ: .
6) Катет, лежащий напротив угла с градусной величиной 30°, равен половине гипотенузы. Пусть - гипотенуза этого треугольника. По теореме Пифагора:
Больше сделать здесь ничего нельзя, поскольку длина гипотенузы нам не дана. Но если бы она была дана, то длину катета можно было бы вычислить через эту формулу.
Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию равнобедренного треугольника, совпадают между собой. Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны." Решение: Итак, треугольники АМD и DNC - равны между собой, так как AD=DC (BD- медиана), NC=МA (так как МВ=BN - дано, а АВ=ВС - треугольник АВС равнобедренный) и улы ВАС и ВСА между равными сторонами равны. Из равенства тр-ков вытекает равенство сторон МD и ND. Что и требовалось доказать
1) По теореме Пифагора:
ответ: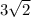 .
.
2) По теореме Пифагора:
ответ: 8.
3) Диагональ квадрата равна произведению его стороны на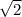 , тогда:
, тогда:
ответ: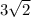 .
.
4) По теореме Пифагора:
Площадь прямоугольного треугольника равна полупроизведению его катетов.
ответ: 6; 24.
5) Треугольник равнобедренный (по условию). В равнобедренном треугольнике высота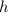 является биссектрисой и медианой. Образовавшиеся два треугольника являются прямоугольными. По теореме Пифагора:
является биссектрисой и медианой. Образовавшиеся два треугольника являются прямоугольными. По теореме Пифагора:
ответ: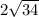 .
.
6) Катет, лежащий напротив угла с градусной величиной 30°, равен половине гипотенузы. Пусть - гипотенуза этого треугольника. По теореме Пифагора:
- гипотенуза этого треугольника. По теореме Пифагора:
Больше сделать здесь ничего нельзя, поскольку длина гипотенузы нам не дана. Но если бы она была дана, то длину катета можно было бы вычислить через эту формулу.
можно было бы вычислить через эту формулу.