Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
dilyakon
01.09.2020 23:02 •
Геометрия
Найдите площадь фигуры, ограниченной линиями
Показать ответ
Ответ:
СергейПеро
17.06.2020 19:10
то есть нам надо интеграрировать потом находить площадь \int\limits^a_b {x} \, dx
единиц
0,0
(0 оценок)
Ответ:
milanagorbovsk
17.06.2020 19:10
0,0
(0 оценок)
Популярные вопросы: Геометрия
German1224
09.06.2020 08:15
Надо в третьем и четвертом упражнении написать дано решение и т.д. Надо сделайте весь тест У МЕНЯ МАЛО ВРЕМЕНИ ПОБЫСТРЕЕ...
вампир982
22.10.2021 04:59
Основные тригонометрические тождества. Урок 2Упрости: (1 – cos218°) ∙∙∙ cos78°....
hcggchhcfuj
11.12.2021 07:52
Наведіть прикладипаралельних лінійз навколишнього середовища...
lubovmarkina3
01.03.2021 10:19
Даны точки A(4;6) и B(4;12). Найди координаты точек C и D, если известно, что точка B — середина отрезка AC, а точка D — середина отрезка BC. C=( ) ( ) D=( ) ( )...
Аккаунт удален
17.11.2022 07:04
Сумма катетов прямоугольного треугольника равна 20 см, гипотенуза равна 16см.Найдите радиус окружности, вписанной в этот треугольник. ...
Superniolay
07.01.2023 14:46
Какие треугольники равны? Верных ответов: 2F и DA и DB и FA и CF и EC и DНашли ошибку на сайте?...
lala70
26.02.2021 07:19
Найди пары равных треугольников и докажите их равенство...
МарияПу16
26.02.2021 07:19
Паралельні прямі a і b перетинають сторони кута. Знайдіть x...
чтотакоеаудирование
15.09.2022 21:45
Вычисли площадь треугольника АВС, если АВ 3м, ВС — 8МиZB- 30°....
Sergei12121
13.09.2021 05:22
Sabcd - правильная пирамида ad=sd=4 m наибольшая стопорона сечения пирамиды плоскостью альфа найти m^2...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
то есть нам надо интеграрировать потом находить площадь \int\limits^a_b {x} \, dx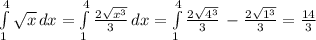 единиц
единиц