№1 1) |_EAD=|_BEA-накрест лежащие при параллельных прямых BC и AD, следовательно |_BAE=|_BEA,так как треугольник BEA-равнобедренный (по условию), и углы при основании равны по 30 градусов. 2) BAE=180-(30+30)=180-60=120 градусов 3) |_В параллелограмме противоположные углы равны, значит |_D=|_B=120 градусов 4) |_C=30+30=60 градусов ответ:|_C=60 градусов; |_D=120 градусов №2 1) P(параллелограмма)=(AB+BC)*2 2) BC=BK+KC=18+10=28 3)AB=BK, так как биссектриса делит угол на два, и |_KAD=|_BAK=BKA, так как треугольник ABK-равнобедренный 4) Значит AB=BK=18 5) P=(28+18)*2=92 ответ:92
Точки A, B, C, D не лежат в одной плоскости. К и M - точки пересечения медиан треугольников АCD и BCD соответственно. Докажите, что четырехугольник АКМВ является трапецией. Вычислите длину отрезка КМ, если AB 27 CM. Сделайте с рисунком.
Объяснение:
1) Пусть медиана АК , ΔСDA , пересечет сторону АD в точке О, СО=ОD.
В ΔСDB соединим О с В, ОВ- медиана , М-точка пересечения медиан.
По т. о точке пересечения медиан имеем
ΔСDA , ,или ;ΔCDB , , или .
ΔОМК подобен ΔОВА по 2-м пропорциональным сторонам и равному углу между этими сторонами :∠О-общий, ⇒соответственные углы равны ∠ОКМ=∠ОАВ , при секущей ОА ⇒ МК║АВ по признаку параллельности прямых.
У четырехугольника АКМВ 2 стороны параллельны ⇒ это трапеция.
2) Т.к. ΔОМК подобен ΔОВА то сходственные стороны пропорциональны или KM=27*1:3=9 (см) .
1) |_EAD=|_BEA-накрест лежащие при параллельных прямых BC и AD, следовательно |_BAE=|_BEA,так как треугольник BEA-равнобедренный (по условию), и углы при основании равны по 30 градусов.
2) BAE=180-(30+30)=180-60=120 градусов
3) |_В параллелограмме противоположные углы равны, значит |_D=|_B=120 градусов
4) |_C=30+30=60 градусов
ответ:|_C=60 градусов; |_D=120 градусов
№2
1) P(параллелограмма)=(AB+BC)*2
2) BC=BK+KC=18+10=28
3)AB=BK, так как биссектриса делит угол на два, и |_KAD=|_BAK=BKA, так как треугольник ABK-равнобедренный
4) Значит AB=BK=18
5) P=(28+18)*2=92
ответ:92
Точки A, B, C, D не лежат в одной плоскости. К и M - точки пересечения медиан треугольников АCD и BCD соответственно. Докажите, что четырехугольник АКМВ является трапецией. Вычислите длину отрезка КМ, если AB 27 CM. Сделайте с рисунком.
Объяснение:
1) Пусть медиана АК , ΔСDA , пересечет сторону АD в точке О, СО=ОD.
В ΔСDB соединим О с В, ОВ- медиана , М-точка пересечения медиан.
По т. о точке пересечения медиан имеем
ΔСDA ,ΔОМК подобен ΔОВА по 2-м пропорциональным сторонам и равному углу между этими сторонами :∠О-общий,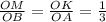 ⇒соответственные углы равны ∠ОКМ=∠ОАВ , при секущей ОА ⇒ МК║АВ по признаку параллельности прямых.
⇒соответственные углы равны ∠ОКМ=∠ОАВ , при секущей ОА ⇒ МК║АВ по признаку параллельности прямых.
У четырехугольника АКМВ 2 стороны параллельны ⇒ это трапеция.
2) Т.к. ΔОМК подобен ΔОВА то сходственные стороны пропорциональны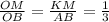 или KM=27*1:3=9 (см) .
или KM=27*1:3=9 (см) .