по правилу треугольника сумма любых двух сторон треугольника больше третьей
пусть х третья сторона треугольника;
тогда
3.7+х>9.4;
9.4+х >3.7
3.7+9.4> х
из третьего условия следует, что х меньше 13.1;
а из первого х >5.7, а
значит, 5.7<х<13.1 , второе условие при этом ограничении справедливо.
Все вычисления в дециметрах производились.
И все же склонен к мысли о том, что задача звучит не совсем корректно, поскольку, если бы нужно было найти наибольшее и наименьшее целые, то был бы ответ на Ваш вопрос 13 и 6, а так ответ остается открытым.
Пусть прямая СЕ проходит через вершину С параллелограмма ABCDE и делит его сторону на отрезки АЕ и ЕD. При этом образуются треугольник ECD и четырехугольник ABCE. Поскольку BC║AE, этот четырехугольник является трапецией.
Пусть АЕ = а, ЕD = b.
Тогда ВС = а + b.
Проведем высоту трапеции к ее основанию a и высоту треугольника к его стороне b.
Эти высоты будут равны, как противоположные стороны образованного прямоугольника.
Чтобы найти площадь треугольника, нужно произведение стороны на высоту, проведенную к ней, разделить пополам.
Значит, .
Чтобы найти площадь трапеции, нужно умножить половину суммы ее оснований на высоту.
Значит, .
По условию, площади относятся как 1:2.
Отсюда, имеем:
.
По свойству пропорции, произведение ее крайних членов равно произведению средних:
.
ответ: прямая делит сторону параллелограмма в отношении 2:1.
по правилу треугольника сумма любых двух сторон треугольника больше третьей
пусть х третья сторона треугольника;
тогда
3.7+х>9.4;
9.4+х >3.7
3.7+9.4> х
из третьего условия следует, что х меньше 13.1;
а из первого х >5.7, а
значит, 5.7<х<13.1 , второе условие при этом ограничении справедливо.
Все вычисления в дециметрах производились.
И все же склонен к мысли о том, что задача звучит не совсем корректно, поскольку, если бы нужно было найти наибольшее и наименьшее целые, то был бы ответ на Ваш вопрос 13 и 6, а так ответ остается открытым.
Пусть прямая СЕ проходит через вершину С параллелограмма ABCDE и делит его сторону на отрезки АЕ и ЕD. При этом образуются треугольник ECD и четырехугольник ABCE. Поскольку BC║AE, этот четырехугольник является трапецией.
Пусть АЕ = а, ЕD = b.
Тогда ВС = а + b.
Проведем высоту трапеции к ее основанию a и высоту треугольника к его стороне b.
Эти высоты будут равны, как противоположные стороны образованного прямоугольника.
Чтобы найти площадь треугольника, нужно произведение стороны на высоту, проведенную к ней, разделить пополам.
Значит,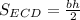 .
.
Чтобы найти площадь трапеции, нужно умножить половину суммы ее оснований на высоту.
Значит,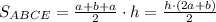 .
.
По условию, площади относятся как 1:2.
Отсюда, имеем:
По свойству пропорции, произведение ее крайних членов равно произведению средних:
ответ: прямая делит сторону параллелограмма в отношении 2:1.