В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды
Объяснение:
Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.
Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.
S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁= Пусть Р₁К⊥ОР, тогда КР=а- =
Так как плоскость АВ₁С₁ пересекает параллельные плоскости по параллельным прямым, то проводим DC₁||AB₁
Плоскость АВ₁С₁ - это плоскость АВ₁С₁D По теореме Пифагора DC₁²=6²+8²=100 DC₁=10 РК- средняя линия треугольника DCC₁ PK=5
PT|| AD и PT || ВС РТ=4
AD⊥CD ⇒ РТ⊥СD AD⊥DD₁ ⇒ РТ⊥ DD₁
РТ перпендикулярна двум пересекающимся прямым плоскости DD₁C₁C, значит перпендикулярна любой прямой лежащей в этой плоскости, в том числе прямой РК РТ⊥ РК Аналогично, МТ ⊥МК Сечение представляет собой прямоугольник Р(cечения)=Р( прямоугольника ТМКР)=2·(4+5)=18
В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды
Объяснение:
Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.
Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.
S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁=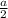
Пусть Р₁К⊥ОР, тогда КР=а- 
=
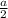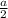
Из ΔКРР₁ по т. Пифагора Р₁К=√(а²+(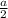
)²)=а√
=
.
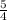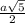S( бок. усеч. пир.)=4*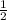
*
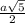*(a+2a)=3a²√5 (ед²).
Плоскость АВ₁С₁ - это плоскость АВ₁С₁D
По теореме Пифагора DC₁²=6²+8²=100
DC₁=10
РК- средняя линия треугольника DCC₁
PK=5
PT|| AD и PT || ВС
РТ=4
AD⊥CD ⇒ РТ⊥СD
AD⊥DD₁ ⇒ РТ⊥ DD₁
РТ перпендикулярна двум пересекающимся прямым плоскости DD₁C₁C, значит перпендикулярна любой прямой лежащей в этой плоскости, в том числе прямой РК
РТ⊥ РК
Аналогично, МТ ⊥МК
Сечение представляет собой прямоугольник
Р(cечения)=Р( прямоугольника ТМКР)=2·(4+5)=18