Нужна , я знаю вы сможете это решить
нужно!
-векторы а b c компланарны если:
1) векторы b и c коллинеарны
2) векторы b и c коллинеарны
3)вектор a равен вектору b
4) вектор c нулевой

-дан abcda1b1c1d1 - параллелепипед. определите тройку компланарных векторов
а) ав,вс,ас
б) db,db,b1d1
в) cb1,cb,ca
г) db, db1, cc1

Показать ответ

Ответ:

kravchenjatkop00zs0

17.10.2020 15:23

Для любой правильной призмы справедливы формулы:

Площадь боковой поверхности:

Sбок = Pосн · h, где

Росн - периметр основания,

h - высота.

Площадь полной поверхности:

Sполн = Sбок + 2Sосн

Объем:

V = Sосн · h

____________________

a - сторона основания.

____________________

Правильная треугольная призма:

в основании лежит правильный треугольник, значит

Sосн =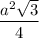 $\dfrac{a^{2}\sqrt{3}}{4}$

Sбок = 3а · h

Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2

$V=\dfrac{a^{2}\sqrt{3}}{4}\cdot h$

____________________

Правильная четырехугольная призма:

в основании - квадрат, значит

Sосн = a²

Sбок = 4ah

Sполн = 4ah + 2a²

V = a²h

____________________

Правильная шестиугольная призма:

Sосн =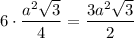 $6\cdot \dfrac{a^{2}\sqrt{3}}{4}=\dfrac{3a^{2}\sqrt{3}}{2}$

Sбок = 6ah

Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3

$V=\dfrac{3a^{2}\sqrt{3}}{2}\cdot h$

0,0(0 оценок)

Ответ:

valeriarodriger

24.04.2022 23:37

На рисунке обозначены:

ABC - Основание пирамиды

OS - Высота

KS - Апофема

OK - радиус окружности, вписанной в основание

AO - радиус окружности, описанной вокруг основания правильной треугольной пирамиды

SKO - двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)

Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).

Свойства правильной треугольной пирамиды:

боковые ребра правильной пирамиды равны

все боковые грани правильной пирамиды являются равнобедренными треугольниками

в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу

если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).

площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан

0,0(0 оценок)

Популярные вопросы: Геометрия