Один из углов равнобедренного тупоугольного треугольника на 111 градусов больше другого. Найдите большой угол этого треугольника. ответ дайте в градусах
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то треугольники подобны.
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ . Доказать: ΔАВС подобен ΔА₁В₁С₁. Доказательство: Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) . Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках: АВ₂ : А₁В₁ = АС : А₁С₁. Сравним полученную пропорцию с данной в условии: АВ : А₁В₁ = АС : А₁С₁ Значит, АВ₂ = АВ. Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию). Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит ΔАВС подобен ΔА₁В₁С₁. Доказано.
Наш треугольник прямоугольный и один из углов 45°, значит третий угол треугольника равен 90° - 45° = 45°.
Получается, что в треугольнике 2 равных угла по 45°, следовательно данный треугольник равнобедренный, следовательно катеты и равны, то есть второй катет тоже 8 см.
Гипотенузу находим по теореме Пифагора:
(см)
P.S
Признак равнобедренного треугольника: если два угла треугольника равны, то такой треугольник равнобедренный
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ .
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) .
Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках:
АВ₂ : А₁В₁ = АС : А₁С₁.
Сравним полученную пропорцию с данной в условии:
АВ : А₁В₁ = АС : А₁С₁
Значит, АВ₂ = АВ.
Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию).
Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит
ΔАВС подобен ΔА₁В₁С₁.
Доказано.
8см,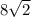 см
см
Объяснение:
Наш треугольник прямоугольный и один из углов 45°, значит третий угол треугольника равен 90° - 45° = 45°.
Получается, что в треугольнике 2 равных угла по 45°, следовательно данный треугольник равнобедренный, следовательно катеты и
и 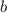 равны, то есть второй катет тоже 8 см.
равны, то есть второй катет тоже 8 см.
Гипотенузу находим по теореме Пифагора:
находим по теореме Пифагора:
P.S
Признак равнобедренного треугольника: если два угла треугольника равны, то такой треугольник равнобедренный
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов