Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.
б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.
б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит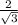
Объяснение: