Онда CD кес 1.2. Түзу бойынан А және В екі нүктесін алып, АВ
кесіндісінің ортасын көз мөлшерімен белгілеңдер. Белгіленген
нүктенің дұрыстығын сызғышты пайдаланып тексеріңдер.
с никтесі бір түзу бойында жатады. АВ​

Треугольник АВС. Провести высоту из вершины В к основанию АС. Поделить высоту ВН пополам. Назовем середину О. Провести прямую, параллельную основанию АС, через точку О. Сторону АВ прямая пересечет в точке D, ВС - в точке F. Разрежем треугольник по отрезкам DF и ОН. Образуются треугольник DBF и два четырехугольника - ADOH и HOFC. Перевернуть треугольник углом В вниз, повернуть 4-угольники сторонами АD и FC внутрь. Соединить BF и AD, BD и FC Получится прямоугольник, у которого короткая сторона равна ОВ, а длинная - АС.

Объяснение:

Дано: АВСD - равнобедренная трапеция, АС⊥ВD, КМ - высота трапеции, КМ=12 см, АВ=СD=15 см.

Найти: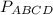

Рассмотрим ΔOBC и ΔAOD. Они прямоугольные, т.к. ∠BOC=∠AOD=90°.

В равнобедренной трапеции диагонали равны, а высота, проведенная через точку пересечения диагоналей является осью симметрии трапеции.

Следовательно ВО=ОС и АО=OD.

Значит ΔOBC и ΔAOD равнобедренные.

ОК - медиана ΔOBC, проведенная из вершины прямого угла. Следовательно ВК=КС=КО.

ОМ - медиана ΔAOD, проведенная из вершины прямого угла.

Следовательно ОМ=АМ=МD.

КМ=КО+ОМ=ВК+АМ.

ВК+АМ - это полусумма оснований.

Значит сумма оснований трапеции будет в два раза больше КМ, т.е. ее высоты.

ВС+АD = 2*МК = 2*12 = 24