Определи площадь треугольника , если = 16 см, ∡=30°, ∡=85°. = см2(все приблизительные числа в расчётах округли до десятитысячных, ответ округли до сотых).
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.
В кубе это боковые ребра и ребра оснований, не имеющие общих точек с боковыми ребрами.
АА1 и CD - скрещивающиеся ребра.
Отрезок, соединяющий середины этих ребер - отрезок РН, где точка Р - середина ребра АА1, а точка Н - середина ребра CD. Тогда по Пифагору:
Что- то мало баллов. :) Обозначим за с=АВ=10 см меньшую хорду (с - так как лежит напротив угла С). а=ВС=12 см - большую сторону (а - так как лежит напротив угла А). Неизвестной останется только сторона b=АС (b - так как лежит напротив угла В). Тогда АВС - треугольник, вписанный в окружность. Пусть AL=LB - середина стороны AB. Точка К - принадлежит стороне BC, причем BK=3 см и согласно условию задачи. Тогда треугольник BKL - прямоугольный. Нетрудно понять по теореме Пифагора, что сторона
LK=4.
Тогда по определению
.
Чтобы найти радиус описанной окружности воспользуемся частью теоремы синусов
5b=8R
Чтобы вычислить b=AC придется применить теорему косинусов.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек или другими словами это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.
В кубе это боковые ребра и ребра оснований, не имеющие общих точек с боковыми ребрами.
АА1 и CD - скрещивающиеся ребра.
Отрезок, соединяющий середины этих ребер - отрезок РН, где точка Р - середина ребра АА1, а точка Н - середина ребра CD. Тогда по Пифагору:
АН = √(AD²+DH²) = √(а²+(а²/4)) =а√5/2.
РН = √(AР²+АH²) = √(а²/4+5а²/4) =а√6/2.
ответ: РН = а√6/2 ед.
Что- то мало баллов. :) Обозначим за с=АВ=10 см меньшую хорду (с - так как лежит напротив угла С). а=ВС=12 см - большую сторону (а - так как лежит напротив угла А). Неизвестной останется только сторона b=АС (b - так как лежит напротив угла В). Тогда АВС - треугольник, вписанный в окружность. Пусть AL=LB - середина стороны AB. Точка К - принадлежит стороне BC, причем BK=3 см и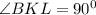
согласно условию задачи. Тогда треугольник BKL - прямоугольный. Нетрудно понять по теореме Пифагора, что сторона
LK=4.
Тогда по определению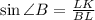
Чтобы найти радиус описанной окружности воспользуемся частью теоремы синусов
5b=8R
Чтобы вычислить b=AC придется применить теорему косинусов.
По определению
AC=10
b=10.
Подставляю в формулу (1)
R=6,25
ответ: радиус окружности равен 6,25 см.