По условию, FBDE - ромб ⇒ FB = BD = DE = FE и ∠DBE = ∠BFE.
Пусть , BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.
Отрезок АС виден под прямыми углами, следовательно, точки A, F, D, C лежат на окружности ⇒ DE - медиана и радиус окружности, следовательно, DE = EC ⇒ ΔDEC - равнобедренный ⇒
∠EDC = ∠DCE = α. Тогда ∠DBE = 180° - α. Известно, что сумма углов четырехугольника равна 360°.
2∠FBD + 2∠DBE = 360°
2∠FBD + 360° - 2α = 360°
∠FBD = α
Таким образом, ∠A = ∠B = ∠C ⇒ ΔABC - равносторонний.
По условию, FBDE - ромб ⇒ FB = BD = DE = FE и ∠DBE = ∠BFE.
Пусть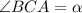
, BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.
Отрезок АС виден под прямыми углами, следовательно, точки A, F, D, C лежат на окружности ⇒ DE - медиана и радиус окружности, следовательно, DE = EC ⇒ ΔDEC - равнобедренный ⇒
∠EDC = ∠DCE = α. Тогда ∠DBE = 180° - α. Известно, что сумма углов четырехугольника равна 360°.
2∠FBD + 2∠DBE = 360°
2∠FBD + 360° - 2α = 360°
∠FBD = α
Таким образом, ∠A = ∠B = ∠C ⇒ ΔABC - равносторонний.
Sполн = 16(12+√3)/3 см².
Объяснение:
∠АС1С = 30° (по сумме острых углов прямоугольного треугольника).
АС = 4см (катет против угла 30°).
СС1 = 4√3см (второй катет треугольника АС1С).
∠АВО = 60° (диагонали ромба - биссектрисы).
∠АВО = 30° ( второй острый угол - диагонали ромба взаимно перпендикулярны).
ВО = АВ/2 как катет против угла 30°.
АВ = 4√3/3 см; ВО = 2√3/3см (по Пифагору). BD = 4√3/3см.
Sabcd = (1/2)·AC·BD = (1/2)·4·4√3/3 = 8√3/3см².
Sграни = АВ·СС1 = 4√3/3·4√3 = 16см².
S = 2·Sabcd+4·Sграни = 16√3/3 +4·16 = 16(12+√3)/3 см².