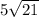Периметр ромба равен 8 м.
Объяснение:
В ромбе диагонали взаимно перпендикулярны и являются биссектрисами углов. Следовательно ∠KEL = ∠EKL.
∠EOA = ∠EKL (дано). =>
∠KEL = ∠EAO => треугольник EOA равнобедренный.
Кроме того, АВ║LK║EF (так ∠EOA = ∠EKL соответствкнные углы при АВ и LK и секущей ЕК).
Значит ЕА = АО =1м.
АО = ОВ (так как точка О - точка пересечения диагоналей ромба).
AEFB - параллелограмм (так как АВ║EF и EA║FB). =>
EF =AB = 2·AO = 2 м.
Итак, сторона ромба равна 2м, тогда его периметр равен 8м (стороны ромба равны).
Задача № 1.
Дано:
Решение: Так как ABC - прямоугольный треугольник, то AB можно найти по теореме Пифагора:
ответ: 5.
Задача № 2.
Решение: Так как NMK - прямоугольный треугольник, то NK можно найти по теореме Пифагора:
ответ:
Задача № 3.
Решение: так как RKL - прямоугольный треугольник, то RL найдем через теорему Пифагора:
Задача № 4.
Дано: ∠M = 30°,
Решение: MNS - прямоугольный треугольник:
1. Так как катет NS лежит напротив 30 градусов, то он равен половине гипотенузы:
2. Найдем катет MS через теорему Пифагора:
ответ: 3
Задача № 5.
Решение: Рассмотрим треугольник BDC - прямоугольный:
- так как высота делит основание пополам в равнобедренном треугольнике
BD найдем по теореме Пифагора:
ответ: 15
Задача № 6.
Дано: ΔRMN - правильный,
Решение: Рассмотрим ΔRKN - прямоугольный:
1. Высота делит основание пополам в правильном треугольнике:
2. Найдем высоту по теореме Пифагора:
Задача № 7.
Дано: ΔMPR - правильный,
Решение: Рассмотрим ΔPTR - прямоугольный:
1. Высота делит основание пополам, тогда:
2. Найдем PR через теорему Пифагора:
Отрицательный корень нам не подходит, так как длина отрезка не может быть отрицательной.
Задание № 8.
Решение: Рассмотрим ΔACD - прямоугольный:
Найдем CD по теореме Пифагора:
Периметр ромба равен 8 м.
Объяснение:
В ромбе диагонали взаимно перпендикулярны и являются биссектрисами углов. Следовательно ∠KEL = ∠EKL.
∠EOA = ∠EKL (дано). =>
∠KEL = ∠EAO => треугольник EOA равнобедренный.
Кроме того, АВ║LK║EF (так ∠EOA = ∠EKL соответствкнные углы при АВ и LK и секущей ЕК).
Значит ЕА = АО =1м.
АО = ОВ (так как точка О - точка пересечения диагоналей ромба).
AEFB - параллелограмм (так как АВ║EF и EA║FB). =>
EF =AB = 2·AO = 2 м.
Итак, сторона ромба равна 2м, тогда его периметр равен 8м (стороны ромба равны).
Объяснение:
Задача № 1.
Дано: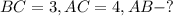
Решение: Так как ABC - прямоугольный треугольник, то AB можно найти по теореме Пифагора:
ответ: 5.
Задача № 2.
Дано: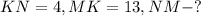
Решение: Так как NMK - прямоугольный треугольник, то NK можно найти по теореме Пифагора:
ответ: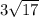
Задача № 3.
Дано: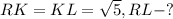
Решение: так как RKL - прямоугольный треугольник, то RL найдем через теорему Пифагора:
ответ: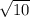
Задача № 4.
Дано: ∠M = 30°,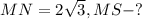
Решение: MNS - прямоугольный треугольник:
1. Так как катет NS лежит напротив 30 градусов, то он равен половине гипотенузы:
2. Найдем катет MS через теорему Пифагора:
ответ: 3
Задача № 5.
Дано: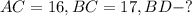
Решение: Рассмотрим треугольник BDC - прямоугольный:
BD найдем по теореме Пифагора:
ответ: 15
Задача № 6.
Дано: ΔRMN - правильный,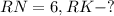
Решение: Рассмотрим ΔRKN - прямоугольный:
1. Высота делит основание пополам в правильном треугольнике:
2. Найдем высоту по теореме Пифагора:
ответ: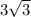
Задача № 7.
Дано: ΔMPR - правильный,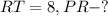
Решение: Рассмотрим ΔPTR - прямоугольный:
1. Высота делит основание пополам, тогда:
2. Найдем PR через теорему Пифагора:
Отрицательный корень нам не подходит, так как длина отрезка не может быть отрицательной.
ответ: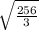
Задание № 8.
Дано: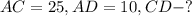
Решение: Рассмотрим ΔACD - прямоугольный:
Найдем CD по теореме Пифагора:
ответ: