ОТВЕТЬТЕ НУЖНО 2. Как расположены точки A(-5; 1) B(3; -2) относительно окружности (x+2)²+(y-1)²=9.
3. Напишите уравнение окружности с центром в точке C(5; -3), радиусом 6ед.
4. Напишите уравнение окружности с центром в точке B(-2; 1), проходящей через точку A(0; -3).
5. Напишите уравнение окружности с диаметром MN, если M(-2; -1) N
(4; -3).
Пусть центр верхнего основания O, а ABCD - это плоскость сечения. Отрезок AB принадлежит верхнему основанию, CD - нижнему. Так как рассматриваемая фигура - цилиндр, то AD=BC=6см
Чтобы найти площадь сечения, надо найти AB.
Рассмотрим верхнее основание. Построим из точки O перпендикуляр к отрезку AB. Пусть K - точка пересечения перпендикуляра и AB. По условию, OK=6см
А так как треугольник AOB - равнобедренный, то AK=BK
Рассмотрим треугольник OAK. Он прямоугольный, угол AKO=90 градусов
По теореме Пифагора
Из условия задачи OA=10см
Находим AK:
AB=2*AK=16см
Находим площадь сечения:
S=AB*AD=16*6=96см^2
ответ: площадь сечения равна 96см^2.
Обозначим призму буквами ABCA1B1C1, где ABC - нижнее основание, A1B1C1 - верхнее основание. Рассмотрим прямоугольный треугольнки ABC. Пусть угол ABC=90 градусов, угол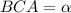
Сторона AC=c по условию задачи. Находим стороны AB и BC.
Так как AC - гипотенуза прямоугольного треугольника ABC, то большая боковая грань призмы - это AA1C1C. По условию угол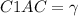
Рассмотрим треугольник C1AC. Он прямоугольный, так как призма - прямая. Угол C1CA=90 градусов. Находим сторону C1C:
Так как призма прямая, CC1=AA1=BB1
Теперь, когда мы знаем все стороны призмы, можно вычислить площадь поверхности. Площадь поверхности равна сумме площадей сторон призмы.
Площадь поверхности призмы равна: