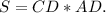Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника:
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: .
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны:
Формула вычисления любой стороны прямоугольника, зная диагональ:
а В математике его называют «куб».
Рассмотрим это геометрическое тело.

Поверхность куба состоит из квадратов.
У квадрата все стороны равны.
Все квадраты, из которых состоит поверхность куба, одинаковы.
Их называют гранями.
Поэтому куб называют многогранником.
У куба 6 граней.

У каждой грани есть стороны.
Стороны называют ребрами.
У куба 12 ребер.
Каждое ребро относится к двум граням куба.
Так как у квадрата все стороны равны, то и все грани куба имеют одинаковую длину.
Концы ребер называются вершинами.
Каждое ребро соединяет две вершины.
Вершин у куба – 8.
Грань, ребро, вершина – это элементы куба.
В одной вершине сходится 3 ребра, каждая грань имеет 4 соседних грани, у каждой грани – 4 ребра.
Возьмем куб, выполненный из бумаги. Попробуем его развернуть. Получится развертка куба.

Развертка – это выкройка куба.
Она состоит из 6 квадратов, расположенных в таком порядке, что из них можно сложить или склеить модель куба.
Перейдем к практической части.
Как изобразить куб на плоскости, например, на листе бумаги?
Куб – объемный предмет. Если обвести основание куба – получится квадрат. Это не является изображением куба.
Для наглядного изображения куба достаточно показать три его грани, например, верхняя, правая и передняя. Также можно сделать чертеж куба.

Для выполнения чертежа построим сначала переднюю грань, сзади выше и правее - заднюю грань, проведем нижние и верхние ребра боковых граней.
Ребра, которые не видны, изображают пунктирной линией, остальные сплошной линией.
Отметим, что на рисунке и чертеже мы не можем передать реальные размеры всех ребер куба.
Итак, в этом уроке Вы познакомились с геометрическим телом «куб», а также научились его изображать на плоскости.
10.
Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника: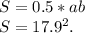
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: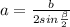 .
.
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны: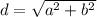
Формула вычисления любой стороны прямоугольника, зная диагональ: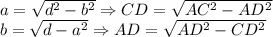
Формула вычисления площади прямоугольника: