Начнем с того, что подкоренные выражения всегда больше или равны нулю, следовательно наименьшее значение корня, которое мы сможем получить=0.Но, данные выражения одновременно равны быть нулю не могут:
Доказательство: предположим, что оба корня равны нулю, значит:
Мы можем увидеть, что x и y принимают разные значения в одном промежутке времени, а следовательно, обе части выражения не могут быть равны нулю, а следовательно возьмем одну пару из двух наименьших возможных значений: x=0,y=1:
Объяснение:
Начнем с того, что подкоренные выражения всегда больше или равны нулю, следовательно наименьшее значение корня, которое мы сможем получить=0.Но, данные выражения одновременно равны быть нулю не могут:
Доказательство: предположим, что оба корня равны нулю, значит: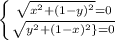
Мы можем увидеть, что x и y принимают разные значения в одном промежутке времени, а следовательно, обе части выражения не могут быть равны нулю, а следовательно возьмем одну пару из двух наименьших возможных значений: x=0,y=1:
ответ: треугольник не существует.
Объяснение:
МК - серединный перпендикуляр к стороне АВ.
Все точки серединного перпендикуляра к отрезку равноудалены от концов отрезка, значит
АК = ВК.
Pbkc = BC + KC + ВК
50 = 11 + KC + ВК
KC + ВК = 50 - 11 = 39 см
Учитывая, что АК = ВК,
КС + АК = 39 см,
а так как АС = КС + АК, то
АС = 39 см
К сожалению, в условии ошибка, так как в треугольнике каждая сторона должна быть меньше суммы двух других сторон, а по данным задачи
39 > 11 + 11
значит треугольник с такими сторонами не существует.