DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 * *h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 *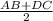
*h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
равновеликих треугольника) = 1/2*S(СDFE)=1/2*10=5 (см²).
S(DAEF)=S(DAE)-S(DFE)=19-5=14 (см²) .