Перпендикуляр, который проведён из вершины прямоугольника к его диагонали, делит прямой угол в отношении 8 : 7. Вычисли острый угол между диагоналями прямоугольника.
ОЧЕНЬ НУЖНО

Перпендикуляр, который проведён из вершины прямоугольника к его диагонали, делит прямой угол в отнош

Показать ответ

Ответ:

kolart

28.03.2021 11:50

Для начала найдем гипотенузу этого треугольника. По теореме Пифагора, квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов его катетов.

$c^2 = a^2 + b^2\\c = \sqrt{a^2+b^2} = \sqrt{(\sqrt{11})^2+5^2} = \sqrt{11+25} = \sqrt{36} = 6$ см.

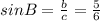Теперь найдем острые углы этого треугольника. Сделаем это через их синусы. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. Пусть угол B лежит напротив катета b. Тогда $sinB = \frac{b}{c} = \frac{5}{6}$ .

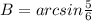Таким образом, $B = arcsin\frac{5}{6}$ ≈ 56,44°.

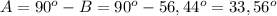Зная это, мы можем найти оставшийся угол А. A = 90^o - B = 90^o - 56,44^o = 33,56^o .

В треугольнике напротив большей стороны всегда лежит больший угол. Значит, наше утверждение правильно. Катет b больше катета a. Поэтому угол B - тот, который лежит напротив катета b, угол A - тот, что лежит напротив катета a.

0,0(0 оценок)

Ответ:

Vlipli779

30.01.2021 08:45

Не знаю, как здесь обозначить вектор. Пусть будет ⁻. То есть, а⁻ - вектор а.

a⁻ (-5; -10); b⁻ (2; 7).

1) a⁻ + b⁻ (-3; -3)

2) 4 · a⁻ (-20; -40)

3) -2 · a⁻ + 3 · b⁻ (16; 41)

4) -b⁻ (-2; -7)

p⁻ (-3; 4); l⁻ (1; 2)

1) p⁻ - l⁻ (-4; 2)

2) Признак коллинеарности векторов: векторы коллинеарны, когда их координаты пропорциональны. Проверяем, вектор (p⁻ - l⁻) имеет координаты (-4; 2), а вектор k - координаты (4; -2).

$\frac{-4}{4} = \frac{2}{-2}\\-1 = -1$