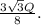Рассмотрим треугольники АОС и ВОД. Они равны по первому признаку равенства треугольников: АО=ОВ и СО=ОД (по условию), угол АОС= углу ВОД (как вертикальные).
Из равенства треугольников следует, что угол САО= углу ОВД, а угол АСО=углу ОДВ. Так как внутренние накрест лежащие углы САО и ОВД, образованные прямыми АС и ВД и секущей АВ, равны, то прямые АС и ВД параллельны, ч.т.д..
Аналогично, так как внутренние накрест лежащие углы АСО и ОДВ, образованные прямыми АС и ВД и секущей СД, равны, то прямые АС и ВД параллельны, ч.т.д..
Для прав. тр-ка центр описанной окр-ти лежит в точке пересеч. высот(медиан, биссектрис). Так как медианы в т. пересеч. делятся в отношении 2:1 считая от вершины, то радиус описанной окружности для прав. тр-ка равен 2/3 от медианы(высоты, биссектрисы). А так как высота прав. тр-ка равна (акор3)/2, то :
О - пересечение АВ и СД
АО=ОВ
СО=ОД
Док-ть: АС || ВД
Док-во:
Рассмотрим треугольники АОС и ВОД. Они равны по первому признаку равенства треугольников: АО=ОВ и СО=ОД (по условию), угол АОС= углу ВОД (как вертикальные).
Из равенства треугольников следует, что угол САО= углу ОВД, а угол АСО=углу ОДВ. Так как внутренние накрест лежащие углы САО и ОВД, образованные прямыми АС и ВД и секущей АВ, равны, то прямые АС и ВД параллельны, ч.т.д..
Аналогично, так как внутренние накрест лежащие углы АСО и ОДВ, образованные прямыми АС и ВД и секущей СД, равны, то прямые АС и ВД параллельны, ч.т.д..
Сторона квадрата равна: корQ
Диагональ квадрата равна: корQ*кор2 = кор(2Q) и равна диаметру описанной окружности.
Значит радиус описанной окружности: R = кор(2Q) /2 = кор(Q/2) (1)
Для прав. тр-ка центр описанной окр-ти лежит в точке пересеч. высот(медиан, биссектрис). Так как медианы в т. пересеч. делятся в отношении 2:1 считая от вершины, то радиус описанной окружности для прав. тр-ка равен 2/3 от медианы(высоты, биссектрисы). А так как высота прав. тр-ка равна (акор3)/2, то :
R = (2/3)*(акор3)/2 = (акор3)/3 (2)
Приравняв (1) и (2), получим:
Площадь тр-ка:
S = (a^2кор3)/4 =