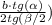Плоскость, проходящая через центр нижнего основания - вопрос №509251 от hardbrain 26.01.2021 11:15

Question

Геометрия: Плоскость, проходящая через центр нижнего основания цилиндра под углом a(альфа) к основанию, пересекает верхнее основание по хорде, равное b и стягивающей дугу b(бэта). найдите высоту цилиндра

hardbrain · Answer

См. рисунок

Дано:

угол С1ОС=альфа

А1В1=b

дуга В1D1А1=бетта

Найти:

D1D=C1C - высоту

С1С можно найти из тангенса альфа:

$tg(\alpha)=\frac{C_{1}C}{OC}$

$C_{1}C=OC*tg(\alpha)$

OC=O1C1

А O1C1 можно найти из тангенса угла А1О1С1:

$tg(A_{1}O_{1}C_{1})=\frac{A_{1}C_{1}}{O_{1}C_{1}}$

$O_{1}C_{1}=\frac{A_{1}C_{1}}{tg(A_{1}O_{1}C_{1})}$

O1D1 - радиус. Тогда А1С1 будет половиной А1В1, т.е. b/2.

Угол А1О1С1 равен половине угла А1О1В1, а угол А1О1В1 является центральным и опирается на дугу В1D1А1 и значит угол А1О1В1=бетта, а угол А1О1С1=бетта/2.

С учетом этого имеем:

$O_{1}C_{1}=\frac{b/2}{tg(\beta/2)}=\frac{b}{2tg(\beta/2)}$

Подставим в формул для нахождения высоты:

$C_{1}C=\frac{b}{2tg(\beta/2})*tg(\alpha)=\frac{b\cdot tg(\alpha)}{2tg(\beta/2})$

ОТВЕТ $\frac{b\cdot tg(\alpha)}{2tg(\beta/2})$

Плоскость, проходящая через центр нижнего основания цилиндра под углом a(альфа) к основанию, пересек