1. Равнобедренный треугольник - треугольник, у которо две стороны равны.
У такого треугольника углы при основании равны.
Биссектриса угла - это луч, делящий данный угол пополам.
Построение биссектрисы угла: 1) берем произвольный раствор циркуля и описываем дугу с центром в вершине угла так, чтобы она пересекала стороны угла 2) этим же раствором проводим дуги с вершиной в точках пересечения исходной дуги со сторонами. Через точку, где эти две новые дуги пересеклись, проводим прямую, которая прохдит и через вершину угла. Полученная прямая и будет биссектрисой угла.
Пусть меньший смежный угол равен х. Тогда другой будет равен 5х. По теореме о сумме смежных углов, получаем: .
Мы нашли меньший угол. Теперь найдем больший: ответ: 30, 150.
Пусть АВ-хорда окружности, а точка О-её центр. Угол АОВ= 120 градусов (по условию). Рассмотрим треугольник АОВ, он равнобедренный, угол АОВ=120 градусов, а два других угла равны (180-120):2=30 градусов. По теореме синусов АО/синус угла АВО=АВ/синус угла АОВ, откуда R=АО=синус 30 градусов*12корней из 3:синус угла АОВ. R=12.
По формуле длины дуги окружности находим: L=число пи*R*120:180=3,14*12*120:180=25,12 (приблизительно, так за число пи берём округлённое его значение). Площадь кругового сектора S=число пи*R в квадрате*120:360=3,14*144*120:360=150,72
1. Равнобедренный треугольник - треугольник, у которо две стороны равны.
У такого треугольника углы при основании равны.
Биссектриса угла - это луч, делящий данный угол пополам.
Построение биссектрисы угла: 1) берем произвольный раствор циркуля и описываем дугу с центром в вершине угла так, чтобы она пересекала стороны угла
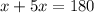
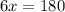
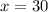 .
.
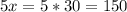
2) этим же раствором проводим дуги с вершиной в точках пересечения исходной дуги со сторонами. Через точку, где эти две новые дуги пересеклись, проводим прямую, которая прохдит и через вершину угла. Полученная прямая и будет биссектрисой угла.
Пусть меньший смежный угол равен х. Тогда другой будет равен 5х. По теореме о сумме смежных углов, получаем:
Мы нашли меньший угол. Теперь найдем больший:
ответ: 30, 150.
Пусть АВ-хорда окружности, а точка О-её центр. Угол АОВ= 120 градусов (по условию).Рассмотрим треугольник АОВ, он равнобедренный, угол АОВ=120 градусов, а два других угла равны (180-120):2=30 градусов.
По теореме синусов АО/синус угла АВО=АВ/синус угла АОВ, откуда R=АО=синус 30 градусов*12корней из 3:синус угла АОВ. R=12.
По формуле длины дуги окружности находим:
L=число пи*R*120:180=3,14*12*120:180=25,12 (приблизительно, так за число пи берём округлённое его значение).
Площадь кругового сектора S=число пи*R в квадрате*120:360=3,14*144*120:360=150,72