по физике 4. Определите выталкивающую силу по рисунку:

А) 4Н

Б) 3Н

В) 16Н

Г) 0,5Н

​

Даны точки A(0;3;-1), B(-1;-2;5), C(1;0;-4), D(-3;-1;-2). Найти:

1) общее уравнение плоскости АВС;

Находим векторы АВ и АС: АВ = (-1; -5; 6), АС = (1; -3; -3).

Их векторное произведение равно:

i         j        k|       i        j

-1      -5        6|     -1      -5

1       -3       -3|      1      -3    =  15i + 6j  + 3k - 3j + 18i + 5k =

                                          = 33i + 3j + 8k.

Нормальный вектор плоскости АВС это (33; 3; 8).

Уравнение плоскости Ax + By + Cz + D = 0.

Подставим координаты точки А:  33*0 + 3*3 + 8*(-1) + D = 0.

1 + D = 0. отсюда D = -1.

Получаем уравнение плоскости АВС: 33x + 3y + 8z - 1 = 0.

2) общее уравнение плоскости, проходящей через точку D параллельно плоскости АВС;

Для параллельной плоскости нормальный вектор сохраняется.

Подставим координаты точки D(-3;-1;-2):

33*(-3) + 3*(-1) + 8*(-2) + D = 0,

-99 - 3 - 16 + D = 0,

-118 + D = 0, отсюда D = 118.

Уравнение 33x + 3y + 8z + 118 = 0.

3) расстояние от точки D до плоскости ABC;

Для вычисления расстояния от точки M(Mx; My; Mz) до плоскости Ax + By + Cz + D = 0

используем формулу:d =   |A·Mx + B·My + C·Mz + D| /√(A² + B² + C²)  

Подставим в формулу данные:

d =   |33·(-3) + 3·(-1) + 8·(-2) + (-1)|/ √(33² + 3² + 8²)  =   |-99 - 3 - 16 - 1|/ √(1089 + 9 + 64)  =    119/ √1162  =   17√1162/166  ≈ 3.49095.

4) канонические уравнения прямой АВ;  точка A(0;3;-1).

Вектор АВ найден выше: АВ = (-1; -5; 6).

Уравнение АВ: x/(-1) = (y - 3)/(-5) = (z + 1)/6.

5) канонические уравнения прямой, проходящей через точку D параллельно прямой AB;  Направляющий вектор АВ(-1; -5; 6) для параллельной прямой сохраняется. Подставляем координаты точки D(-3;-1;-2).

Уравнение : (x + 3)/(-1) = (y + 1)/(-5) = (z + 2)/6.

6) общее уравнение плоскости, проходящей через точку D(-3;-1;-2) перпендикулярно прямой AB.

Вектор АВ (-1; -5; 6) будет нормальным вектором этой плоскости.

Уравнение плоскости Ax + By + Cz + D = 0.

Подставим координаты вектора и точки D:  

(-1)*(-3) + (-5)*(-1) + 6*(-2) + D = 0.

-4 + D = 0. отсюда D = 4.

Уравнение: (-1)x + (-5)y + 6z + 4 = 0 или с положительным коэффициентом перед х:

x + 5y - 6z - 4 = 0.

Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности  , составленный из радиусов проведенных в точки касания ,стягивает дугу  15 см. Найти длину малой окружности.

Объяснение:

Пусть ОА=ОМ=R , CM=CK=r .  По формуле длины дуги      ,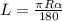

 ⇒ R=  см.  По свойству отрезков касательных ∠АОР=60° .

Пусть СН⊥ОА , тогда ∠НСО=30°.

В ΔНСО по свойству угла 30° :    ОС=2*ОН ,   но   ОС=R+r , ОН=R-r  ,

тогда R+r=2(R-r)   →   r=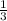 *R  →  r= 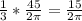(см) .

Длина окружности С=2πr , тогда С=2π*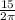 =15 (см) .