Полная поверхность цилиндра равна 520пи см^2,радиус его основания 10 см. на каком расстоянии от оси цилиндра проходит сечение, имеющее форму квадрата.

Объяснение:

1.

1)формула периметра та площі паралелограма

P=2(a+b)

S=ah, h - висота

2)формула периметра та площі прямокутника

P=2(a+b)

S=a* b

3)формула периметра та площі ромба

P=4a

S=ah

4)формула периметра та площі квадрата

P=4a

S=a²

2.

1. Знайдіть площу квадрата якщо його периметр становить 80см

Розвязання

периметр квадрата P=4a, знаходимо а

80=4а, а=80/4=20см - одна сторона квадрата

площа квадрата S=a² ,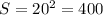 см

2. Знайдіть периметр прямокутника якщо його площа становить 98^2 а одна сторона удвічі більша за іншу

Розвязання

P=2(a+b) - периметр прямокутника

S=a* b - площа прямокутника,за умовою задачі b = 2*a нехай тоді одна сторона прямокутника дорівнює х а друга тоді буде  2х , моємо таке рівняння

2х*х=98

Тобто 1 сторона дорівнює 7 см, доті 2 сторона буде дорівнювати 7*2=14см

Знаходимо периметр

P=2(a+b)

Р=2(7+14)

Р= 42 см

ВСЕ

Задача: В прямоугольном треугольнике ABC угол С = 90°, CH — высота, проведенная к гипотенузе AB, AC = 6 см, AH = 3 см. Найти HB.

Р-м ΔAHC:

∠AHC = 90° (CH — высота к AB) ⇒ΔAHC — прямоугольный.

Катет равен половине гипотенузы, если он лежит против угла в 30°:

катет AH = 3 см, гипотенуза AC = 6 см ⇒ ∠HCA = 30°.

Тогда ∠HAC (∠A) = 90°−∠HCA = 90°−30° = 60°.

Р-м ΔABC:

∠B = 90°−∠A = 90°−60° = 30°.

Катет равен половине гипотенузы, если он лежит против угла в 30°:

катет AC = 6 см, ∠B = 30° ⇒ гипотенуза AB = 2·AC = 2·6 = 12 см.

Тогда отрезок HB = AB−HA = 12−3 = 9 см.

ответ: Длина отрезка HB равна 9 см.