Построить в системе координат отрезок АВ с произвольными координатами точек. Осуществить параллельный перенос отрезка АВ на произвольный вектор а (изобразить его в системе координат)

Задание 1

ответ: Да, существует. Это правильный 8-ми угольник (см. картинку №1).

Объяснение:

Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:

S = 180°(n-2)

Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒

S = 135° × n

Отсюда выходит что:

135n = 180(n-2)

Находим n:

135n = 180n - 360

180n - 135n = 360

45n = 360

n = 360 ÷ 45

n = 8 (количество сторон правильного многоугольника)

Задание 2

ответ: Количество сторон правильного многоугольника = 12 (см. картинку №2).

Объяснение:

Пускай внутренний угол правильного многоугольника = x°

⇒ смежный с ним угол = 0,2x°

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.

⇒ x + 0,2x = 180

1,2x = 180

x = 180 ÷ 1,2

x = 150° (внутренний угол выпуклого многоугольника)

Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:

S = 180°(n-2)

Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒

S = 150° × n

Отсюда выходит что:

150n = 180(n-2)

Находим n:

150n = 180n - 360

180n - 150n = 360

30n = 360

n = 360 ÷ 30

n = 12 (количество сторон правильного многоугольника)

Задание 3

а) ответ: Площадь многоугольника = 64 см².

Объяснение:

Правильный многоугольник, в котором n = 4 это КВАДРАТ.

Диаметр окружности d = 2r, где r - радиус

Известно что сторона квадрата a равна диаметру d вписанной в него окружности

⇒ d = a = 2r = 2×4 = 8 cm.

Площадь квадрата = a² = 8² = 64 cm²

б) ответ: Радиус вписанной окружности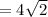 см.

Объяснение:

Известно что сторона квадрата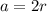 , где r - радиус вписанной окружности.

Так же известно что сторона квадрата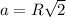 , где R - радиус описанной окружности ⇒

(радиус вписанной окружности)

в) ответ: Периметр многоугольника = 16 см.

Объяснение:

Известно что сторона квадрата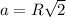 , где R - радиус описанной окружности

⇒

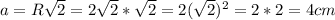
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.

⇒ P = 4 × 4 = 16 cm

Объяснение:

а) Проведем РК║АВ.

РК⊥(ВВ₁С₁), значит В₁К - проекция прямой В₁Р на плоскость (ВВ₁С₁).

ΔВ₁ВК = ΔBCQ по двум катетам, значит

∠1 = ∠2 и ∠3 = ∠4.

∠1 + ∠3 = 90°,  значит в ΔКВМ ∠1 + ∠4 = 90°, следовательно,

∠ВМК = 90°, т.е. В₁К⊥BQ.

Но тогда и B₁P⊥BQ по теореме о трех перпендикулярах.

б)

РК⊥(ВВ₁С₁), значит РК⊥BQ,

BQ⊥B₁K (доказано в п. а), тогда BQ⊥(В₁КР).

Проведем МН⊥В₁Р в треугольнике В₁КР.

Так как МН⊂(В₁КР), то МН⊥BQ и МН⊥В₁Р по построению, тогда

МН - искомое расстояние между прямыми B₁P и BQ.

На выносном рисунке:

ΔВСQ = ΔEC₁Q по катету и острому углу (CQ = C₁Q  и углы при вершине Q равны как вертикальные), ⇒ ЕС₁ = ВС = 3.

ΔВ₁МЕ ~ ΔKMB по двум углам (при вершине М - вертикальные и ∠1 = ∠Е как накрест лежащие при ВС║В₁Е и секущей ВЕ):

    ⇒

Из прямоугольного треугольника В₁ВК по теореме Пифагора:

Из прямоугольного треугольника В₁КР по теореме Пифагора:

ΔB₁MH: