При планировании парка необходимо точно измерить ширину имеющегося водоёма. С геодезистов были размечены вешками точки на поверхности земли. Найдите ширину водоёма, если ОF=200 м , ОВ=10 м , АВ=5 м

1-б 2-а 3 в

Объяснение:

1) угол А1 смежный с углом А2, следовательно его мы можем найти так:180-110=70

Угол С мы можем найти исходя из того, что сумма углов треугольника 180:180-70-40=70

2)угол В1 смежный с углом В2, следовательно его мы можем найти так: 180-160=20

По рисунку видно что второй угол 90 градусов.

Угол А мы можем найти исходя из того, что сумма углов треугольника:180-50-90=40

3) угол С1 смежный с углом С2, следовательно его мы можем найти так:180-150=30

По рисунку видно, что треугольник равнобедренный=>, углы при основании равнв(С=А) =>В=180-(30*2)=120

32 ед².

Объяснение:

Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед.

F∈AA₁, A₁F:FA = 3:4

BC = 4; AB = 2√7; AA₁=14.

Через точки F, B₁,C₁ проходит сечение.

Найти: площадь сечения.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.Противоположные грани параллелепипеда параллельны.

⇒ сечение FB₁C₁C - прямоугольник.

Площадь прямоугольника равна произведению смежный сторон.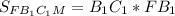

⇒

1. Пусть А₁F = 3x, тогда AF = 4x, а АА₁ = 7х = 14

7х = 14 ⇒ х = 2

Тогда A₁F = 3x = 6

2. Рассмотрим ΔFA₁B₁ - прямоугольный.

A₁F = 6; A₁B₁ = AB = 2√7;

По теореме Пифагора найдем FB₁:

Теперь найдем площадь сечения:

(ед.²)