Сказано. Точка О равноудалена от вершин. То есть проектируется на основание в центр описанной окружности (потому что раз наклонные равны, то и их проекции равны, то есть проекция точки О равноудалена от вершин, то есть это центр описанной окружности). Поэтому расстояние от О до плоскости, радиус описанной окружности и заданное расстояние от О до вершин образуют прямоугольный треугольник, и
H^2 = L^2 - R^2;
L^2 = 410/2; R = 17/2 (ясно, что треугольник Пифагоров 8,15,17, а R равен половине гипотенузы)
H^2 = 205 - 289/4 = 132,75; H = √132,75
Я не буду вычислять, чему равен этот корень, похоже, что в условии ошибка
Sбок= Р*h Sбок=(АВ+ВС+СД ) * АА1
1) т.к угАСВ=90* по условию, и призма прямая, то двугранный угол АСС1В1 =90* . значт угА1СВ=90*
2) рассмотрим треуг А1СВ=прямоуг, угС=90*, СА1В=30*, А1В=10см,
СВ=А1В * sin30* CB=5cm
3) рассмотрим АВС-прямоуг, угС=90* АС=СВ=5см, т.е АВС равнобедренный
по тПифагора АВ= sqrt 2AC^2 AB=5sqrt2
4) рассмотрим АА1В- прямоугольный , угА=90, АВ=5sqrt2 , А1В=10
из тПифагора АА1=sqrt ( A1B^2 -AB^2) AA1=sqrt(100- 50)= 5sqrt2
5) Sбок = (5sqrt2 + 5 + 5 ) * 5 sqrt2 =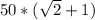 cm
cm
Сказано. Точка О равноудалена от вершин. То есть проектируется на основание в центр описанной окружности (потому что раз наклонные равны, то и их проекции равны, то есть проекция точки О равноудалена от вершин, то есть это центр описанной окружности). Поэтому расстояние от О до плоскости, радиус описанной окружности и заданное расстояние от О до вершин образуют прямоугольный треугольник, и
H^2 = L^2 - R^2;
L^2 = 410/2; R = 17/2 (ясно, что треугольник Пифагоров 8,15,17, а R равен половине гипотенузы)
H^2 = 205 - 289/4 = 132,75; H = √132,75
Я не буду вычислять, чему равен этот корень, похоже, что в условии ошибка
Скорее всего L = (√410)/2
То есть L^2 = 410/4
В этом случае H^2 = 121/4; H = 11/2;