Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
flanyshkatop
14.11.2020 12:23 •
Геометрия
Ребят нужна с этими заданиями.От что у меня есть (55)
Показать ответ
Ответ:
nermakov
15.10.2020 14:41
ответ:
ответ:
ответ:
0,0
(0 оценок)
Популярные вопросы: Геометрия
Maykshmidt
08.02.2021 08:12
Один угол треугольника в 2 раза меньше другого и на 20градусов больше третьего.найдите углы треугольника))...
TimurZel
08.02.2021 08:12
Втреугольнике mnk биссектрисы пересекаются в точке о. расстояние от точки о до стороны mn=6cv,nk=10см.найдите площадь треугольника nok...
LaGGe
14.07.2020 15:22
Радиус описанной около равностороннего треугольника окружности равен 8см. найдите периметр этого треугольника и радиус вписанной окружности. всё подробно т.к. на контрошу (желательно...
ЭммаУаилд
14.07.2020 15:22
Биссектрисы вк и ем треугольника все пересекаются в точке о, отрезок мк паралелен стороне ве. доказать, треугольники ком и вое подобны...
винишко12
14.07.2020 15:22
Утреугольника со сторонами 16 и 8 см,проведены высоты к этим сторонам. высота,проведенная к стороне 16 см, равна 6 см.чему равна высота,проведенная к стороне 8 см?...
raykova568
14.07.2020 15:22
А)катеты прямоугольного треугольника равны 6 см и 8 см.вычислите высоту,проведенную к гипотенузе. б)катеты прямоугольного треугольника равны 3 см и 4 см.вычислите высоту,прооведенную...
Faleck
14.07.2020 15:22
А)две точки делят окружность на дуги,градусные меры которых пропорциональны числам 2 и 7. какова градусная мера каждой из этих дуг? б)точки к и м делят окружность на две дуги,...
тони2006
14.07.2020 15:22
Решить! треуголльник abc -равнобедренный, bd -медиана,к- принадлежит bd, м-принадлежит ав, n-принадлежит вс.угол вкм=углуbkn, уголbmk=110 градусов.найти угол bmk.доказать,что...
zentex
14.07.2020 15:22
Спортивная площадка площадью 32^2метра имеет форму квадрата.лампа освещает круг радиуса,равного высоте,на которой эта лампа подвешена. на какой минимальной высоте (в метрах) следует...
anastasia559
14.07.2020 15:22
Решить! №1. в трапеции abcd точка m - середина большего основания ad, md=bc, угол в = 100 градусов. найти углы amc и bcm. №2. на стороне ad параллелограмма abcd отмечена точка...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
ответ: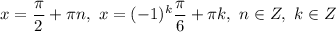
ответ: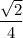
ответ: