AD = (√21)/5 ед.
Объяснение:
Биссектриса AD угла А треугольника АВС делит противоположную сторонуВС в отношении прилежащих сторон.
То есть BD/DC = 4/1. ВС =АВ = 4 ед.
Значит СD = 4/5 ед.
Проведем высоту ВН. В равнобедренном треугольнике АВС высота является и медианой. АН = НС = 1/2 ед.
В прямоугольном треугольнике АВН
CosA = AH/AB = (1/2)/4 = 1/8.
Углы при основании равнобедренного треугольника равны.
CosC = CosA = 1/8.
В треугольнике ADC по теореме косинусов:
AD = √(AC²+DC² - 2·AC·DC·CosC) =>
AD = √(1+16/25 - 2·1·4/5·1/8) => AD = √(21/25).
Объяснение: два решения, так как не знаю какую тему проходите.
1. решение.
Найдем длины сторон.
АВ =
AC =
BC =
По теореме косинусов
BC²=AB²+AC²-2AC*AB*cosA и отсюда
cosA =
Угол А = 45°
2 решение
Найдем координаты векторов
Аналогично АС(-1;-1)
Найдем модули векторов
|AB| =
Аналогично |AC| = кстати, модуль вектора и есть его длина и мы эти длины уже рассчитали выше.
Скалярным произведением двух векторов является сумма произведений соответствующих координат этих векторов.
(AB*AC) = (-2*(-1)) + 0*(-1)) = 2
Тогда из формулы скалярного произведения векторов АВ и АС
cosA = 45°
AD = (√21)/5 ед.
Объяснение:
Биссектриса AD угла А треугольника АВС делит противоположную сторонуВС в отношении прилежащих сторон.
То есть BD/DC = 4/1. ВС =АВ = 4 ед.
Значит СD = 4/5 ед.
Проведем высоту ВН. В равнобедренном треугольнике АВС высота является и медианой. АН = НС = 1/2 ед.
В прямоугольном треугольнике АВН
CosA = AH/AB = (1/2)/4 = 1/8.
Углы при основании равнобедренного треугольника равны.
CosC = CosA = 1/8.
В треугольнике ADC по теореме косинусов:
AD = √(AC²+DC² - 2·AC·DC·CosC) =>
AD = √(1+16/25 - 2·1·4/5·1/8) => AD = √(21/25).
AD = (√21)/5 ед.
Объяснение: два решения, так как не знаю какую тему проходите.
1. решение.
Найдем длины сторон.
АВ =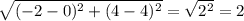
AC =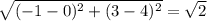
BC =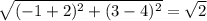
По теореме косинусов
BC²=AB²+AC²-2AC*AB*cosA и отсюда
cosA =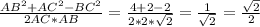
Угол А = 45°
2 решение
Найдем координаты векторов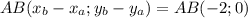
Аналогично АС(-1;-1)
Найдем модули векторов
|AB| =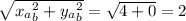
Аналогично |AC| =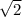
кстати, модуль вектора и есть его длина и мы эти длины уже рассчитали выше.
Скалярным произведением двух векторов является сумма произведений соответствующих координат этих векторов.
(AB*AC) = (-2*(-1)) + 0*(-1)) = 2
Тогда из формулы скалярного произведения векторов АВ и АС
cosA =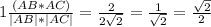
cosA = 45°