с геометрией.. очень нужно. Если вы можете мне периодически с этим , то я буду очень благодарна..
P.S. переведу на русский для ваших удобств: 1. Точка соприкосновения вписанной окружности равнобедренного треугольника делит его боковую сторону в отношении 7: 5 считая от вершины треугольника. Найдите стороны треугольника, если его периметр равен 68см
2. В треугольника с углами 30°, 70° и 80° вписана окружность. Найдите углы треугольника, вершины которого являются точками соприкосновения вписанной окружности к сторонам данного треугольника.
Предположим, что таких сфер конечное количество. Выберем сферу с самым большим радиусом R. Пусть расстояние от центра сферы до плоскости окружности равно d. Тогда расстояние от центра этой сферы до любой из точек окружности равно R=√(r²+d²)
Восстановим перпендикуляр OH к плоскости окружности из ее центра O так, что OH=d1>d. Тогда расстояние от H до любой точки окружности равно R1=√(d1²+r²). Построим сферу с центром в H и радиусом R1. Из наших расчетов эта сфера будет проходить через исходную окружность. Осталось заметить, что R1=√(d1²+r²)>√(d²+r²)=R по построению, т.е. мы построили сферу, проходящую через данную окружность, с радиусом, большим R, несмотря на то, что по предположению это была сфера с самым большим радиусом, и при этом проходящая через данную окружность. Значит наше предположение неверно и таких сфер бесконечное количество.
Бесконечно много.
Объяснение:
Предположим, что таких сфер конечное количество. Выберем сферу с самым большим радиусом R. Пусть расстояние от центра сферы до плоскости окружности равно d. Тогда расстояние от центра этой сферы до любой из точек окружности равно R=√(r²+d²)
Восстановим перпендикуляр OH к плоскости окружности из ее центра O так, что OH=d1>d. Тогда расстояние от H до любой точки окружности равно R1=√(d1²+r²). Построим сферу с центром в H и радиусом R1. Из наших расчетов эта сфера будет проходить через исходную окружность. Осталось заметить, что R1=√(d1²+r²)>√(d²+r²)=R по построению, т.е. мы построили сферу, проходящую через данную окружность, с радиусом, большим R, несмотря на то, что по предположению это была сфера с самым большим радиусом, и при этом проходящая через данную окружность. Значит наше предположение неверно и таких сфер бесконечное количество.
4)
Так как треугольник равнобедренный, то углы при основании — равны.
И так как каждый из них равен 62°, то угол, противолежащий основанию — равен: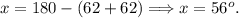
//Надо заметить, что сумма внутренних углов треугольника — всегда равна 180°.//
5)
Чтобы треугольник существовал, сумма каждых двух сторон — должна быть больше каждой оставшийся стороны, тоесть:
Проверим: 7.2+4.3 = 11.5.
Третья сторона не должна быть равна, или больше чила 11.5, тоесть длина оставшийся стороны может максимально равна: 11.499999.
6)
//Нет рисунка//
7) Один из углов треугольника три раза меньше второго и на 150 больше третий. Найдите углы треугольника.
Объявим этот же угол — как переменная "x".
Второй угол, который больше "x" в 3 раза — будет объявлен как: "3x";
Третий угол, который меньше "x" на 150° — будет объявлен как" "x-150".
Составим уравнение:
Как мы видим — один из углов больше суммы всех углов треугольника, а другой-то вообще — отрицательный.
Я опробовала много вариантов, спобом подборки, всё равно не получилось найти целые — соответствующие углам треугольника числа.
Или задача с ошибков, или вот — правильный ответ: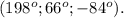
8) Внешний угол равен 105°, что и означает, что внутренний и смежной с ним углов равен: 180-105 = 75°.
По теореме внешнего угла: сумма двух оставшихся внутренних углов, не смежных со внешним углом — равен этому же внешнему углу.
Тоесть сумма двух оставшихся углов равна: x+y = 105°.
Так как их отношения равно — 4:3, то переменные таковы: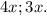
Составим уравнение: