Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что . Проведем прямую . Тогда . Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. , а значит и любой прямой в этой плоскости. Пусть . Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда , а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость . Покажем, что . и , и . Тогда задача сводится к нахождению площади треугольника . Будем искать ее, как . Из подобия треугольников следует, что . Из подобия треугольников . Подставив найденное в формулу выше, получим . Таким нами образом было получено, что искомая площадь равна .
1) Основание остроугольного равнобедренного треугольника равна 30 см, а высота, опущенная на боковую сторону, = 24см. Найти периметр треугольника. 2) Сторона ромба равна 25 см, а его высота- 24 см. Найти диагонали ромба.
1). НС=√(30²-24²)=18см. (по Пифагору). АВ²-ВН²=АН² (по Пифагору). Или 24²=(18+х)²-х². => х=7см. АВ=ВС=18+7=25см. Периметр равен 25+25+30=80см.
2). Площадь ромба равна Sabcd= ВН*AD = 24*25=600см². АН=√(25²-24²)=7см. (по Пифагору). НD=25-7=18см. BD= √(24²+18²)=30см. (по Пифагору). Sabcd=(1/2)*D*d=600см² (найдена ранее) => AC=1200/30=40см. ответ: диагонали ромба равны 40см и 30см.
(см. объяснение)
Объяснение:
Поскольку пирамида правильная, то BH - медиана, биссектриса и высота треугольника ABC, то есть верно, что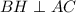
. Проведем прямую 
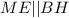. Тогда 
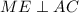. Пусть CP другая медиана треугольника ABC. Пусть медианы этого треугольника пересекаются в точке O. Тогда из-за того, что пирамида правильная, SO - это ее высота, т.е. 
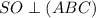, а значит и любой прямой в этой плоскости. Пусть 
. Проведем через точку J прямую параллельную SO, которая пересечет SC в точке I. Тогда 
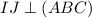, а значит и любой прямой в этой плоскости. Соединим точки M, I и E. Получим плоскость 
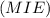. Покажем, что 
. 
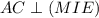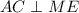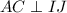и 
, и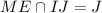 
. Тогда задача сводится к нахождению площади треугольника 
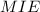. Будем искать ее, как 
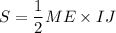. Из подобия треугольников следует, что 
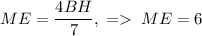. Из подобия треугольников 
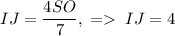. Подставив найденное в формулу выше, получим 
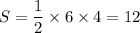. Таким нами образом было получено, что искомая площадь равна 
.
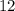Задание выполнено!
Найти периметр треугольника.
2) Сторона ромба равна 25 см, а его высота- 24 см.
Найти диагонали ромба.
1). НС=√(30²-24²)=18см. (по Пифагору).
АВ²-ВН²=АН² (по Пифагору). Или
24²=(18+х)²-х². => х=7см.
АВ=ВС=18+7=25см.
Периметр равен 25+25+30=80см.
2). Площадь ромба равна Sabcd= ВН*AD = 24*25=600см².
АН=√(25²-24²)=7см. (по Пифагору).
НD=25-7=18см.
BD= √(24²+18²)=30см. (по Пифагору).
Sabcd=(1/2)*D*d=600см² (найдена ранее) =>
AC=1200/30=40см.
ответ: диагонали ромба равны 40см и 30см.