SB перпендикулярен плоскости прямоугольника ABCD. а) Докажите, что треугольник ASD прямоугольный б) Если CD = 3 см, AD = 4 см, SB = 5 см, найдите угол между линией SD и плоскостью ABC.

Дан треугольник с вершинами А(3, -7); В(-1, 4); С(-6, -5).

а) Высота из точки А на ВС - перпендикуляр АЕ.

Составляем уравнение стороны ВС: вектор ВС = (-5; -9). Точка В.

ВС: (х + 1)/(-5) = (у - 4)/(-9)  канонический вид

-9x + 5y - 29 = 0                общий вид

у = 1,8х + 5,8                    с угловым коэффициентом.

Угловой коэффициент перпендикулярной прямой к ВС равен:

к = -1/(к(ВС) = -1/(9/5) = -5/9.

Уравнение имеет вид у = (-5/9)х + в.

Для определения в подставим координаты точки А(3,-7).

-7 = (-5/9)*3 + в,

в = -7 + (15/9) = -48/9.

Получаем уравнение ВE:  у = (-5/9)x - (48/9).

б) Середина АС - точка Д((3-6)/2=-1,5; (-7-5)/2=-6) = (-1,5; -6).

Вектор ВД = (-1,5-(-1)=-0,5; (-6-4)/2=-10) = (-0,5; -10)

Уравнение ВД: (х + 1)/(-0,5) = (у - 4)/(-10).

Можно привести к целым числам, умножив знаменатели на -2:

(х + 1)/1) = (у - 4)/20.

Общий вид у - 20х - 24 = 0,

С угловым: у = 20х + 24.

 

Дано :

ΔCDE.

СD = 8 см.

DE = 10 см.

СЕ = 12 см.

Отрезок DK - биссектриса ΔCDE.

Найти :

DK = ?

Пусть СК = х, тогда КЕ = 12 (см) - х.

Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Соответственно -

Подставим всё то, что нам известно и находим х -

- - -

cм

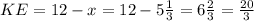см.

Квадрат длины биссектрисы угла треугольника равен произведению сторон, из которых выходит биссектриса, без произведения отрезков, на которая она делит третью сторону.

Запишем в виде формулы -

Осталось только подставить и подсчитать -

см.

(см).