P(ABCD) = 126 см
S(ABCD) = 864 см^2
Объяснение:
Обозначим вершины равнобокой трапеции так, как на рисунке.
O - точка пересечения диагоналей равнобокой трапеции.
По свойству диагоналей равнобокой трапеции AC = BD. Треугольники AOB и BOC равнобедренные. По условию CO:AO = BO:OD = 3:13.
Тогда обозначим AO = DO = 13x, CO = BO = 3x.
Проведем через точку C прямую, параллельную диагонали BD, пусть эта прямая пересекает основание AD в точке P.
BC║DP(так как основания трапеции параллельны), BD ║CP(по построению) ⇒ по определению BCPD - параллелограмм.
По свойству противоположных сторон параллелограмма CP = BC/.
Но при этом BD = AC , так как диагонали равнобокой трапеции равны.
Значит, AC = CP, и треугольник ACP равнобедренный по определению.
AC = AO + OC = 13x + 3x = 16x, CP = AC = 16x
<AOD = <BOC (это вертикальные углы), BO:OD = CO:AO ⇒
⇒ треугольники AOD и BOC подобны по двум сторонам и углу между ними. Поэтому BC:AD = CO;AO = BO:DO = 3:13
Тогда пусть BC = 3a, AD = 13a.
Проводим высоты BK и CH.
BK║CH(высоты), BC║KH(основания трапеции параллельны) ⇒
⇒ по определению BCHK - параллелограмм.
По свойству противоположных сторон параллелограмма BC = KH = 3a
Прямоугольные треугольники ABK и DCH равны по гипотенузе(AB = CD) и острому углу(<BAK = <CDH) ⇒ AK = HD
Тогда KH = AD - AK - HD = AD - 2*AK
Из этого равенства находим AK:
AK = (AD - KH)/2 = (13a - 3a)/2 = 5a
Из прямоугольного треугольника ABH находим, чему равно a:
AB = AD = 13a(по условию большее основание равно боковой стороне)
AH = 5a
BH = = = 12a = 36
a = 3
Периметр трапеции равен:
P(ABCD) = AB + BC + CD + AD = 13a + 3a + 13a + 13a = 42a = 42*3 = 126 см
Площадь трапеции равна произведению полусуммы длин ее оснований на длину высоты трапеции:
S(ABCD) = (AD + BC)/2 * BK = (3a + 13a)/2 * 36 = 8a * 36 = 8*3*36 = 864 см^2
P(ABCD) = 126 см
S(ABCD) = 864 см^2
Объяснение:
Обозначим вершины равнобокой трапеции так, как на рисунке.
O - точка пересечения диагоналей равнобокой трапеции.
По свойству диагоналей равнобокой трапеции AC = BD. Треугольники AOB и BOC равнобедренные. По условию CO:AO = BO:OD = 3:13.
Тогда обозначим AO = DO = 13x, CO = BO = 3x.
Проведем через точку C прямую, параллельную диагонали BD, пусть эта прямая пересекает основание AD в точке P.
BC║DP(так как основания трапеции параллельны), BD ║CP(по построению) ⇒ по определению BCPD - параллелограмм.
По свойству противоположных сторон параллелограмма CP = BC/.
Но при этом BD = AC , так как диагонали равнобокой трапеции равны.
Значит, AC = CP, и треугольник ACP равнобедренный по определению.
AC = AO + OC = 13x + 3x = 16x, CP = AC = 16x
<AOD = <BOC (это вертикальные углы), BO:OD = CO:AO ⇒
⇒ треугольники AOD и BOC подобны по двум сторонам и углу между ними. Поэтому BC:AD = CO;AO = BO:DO = 3:13
Тогда пусть BC = 3a, AD = 13a.
Проводим высоты BK и CH.
BK║CH(высоты), BC║KH(основания трапеции параллельны) ⇒
⇒ по определению BCHK - параллелограмм.
По свойству противоположных сторон параллелограмма BC = KH = 3a
Прямоугольные треугольники ABK и DCH равны по гипотенузе(AB = CD) и острому углу(<BAK = <CDH) ⇒ AK = HD
Тогда KH = AD - AK - HD = AD - 2*AK
Из этого равенства находим AK:
AK = (AD - KH)/2 = (13a - 3a)/2 = 5a
Из прямоугольного треугольника ABH находим, чему равно a:
AB = AD = 13a(по условию большее основание равно боковой стороне)
AH = 5a
BH =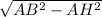
= 
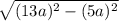= 12a = 36
a = 3
Периметр трапеции равен:
P(ABCD) = AB + BC + CD + AD = 13a + 3a + 13a + 13a = 42a = 42*3 = 126 см
Площадь трапеции равна произведению полусуммы длин ее оснований на длину высоты трапеции:
S(ABCD) = (AD + BC)/2 * BK = (3a + 13a)/2 * 36 = 8a * 36 = 8*3*36 = 864 см^2
P(ABCD) = 126 см