Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
В трапеции ABCD угол A равен 90, градусов, боковая сторона CD перпендикулярна диагонали AC; CD равен 3 см, AD равен 5 см, 1) Найти площадь трапеции. 2) Найти площадь треугольника AMD, если M – середина CD.
1) АВ⊥АD, ВС║AD ⇒ ∠В=90°
СН - высота (ABCD)
Площадь трапеции равна произведению её высоты на полусумму оснований.
S(ABCD)=CH•(BC+AD):2
CH=AC•CD:AD
AC=√(AD²-CD²)=√(5²-3²)=4
CH=3•4:5=2,4 (см)
BC=AH=√(AC²-CH²)=√(16-5,76)=3,2
S(ABCD)=2,4•(3,2+5):2=9,84 см²
* * *
2) Найти площадь треугольника AMD, если M – середина CD.
СМ=MD ⇒АМ - медиана и делит площадь ∆ АСD пополам (свойство).
Можно найти площадь методом нахождения площади всех фигур, при этом прибавив их
Площадь прямоугольника с сторонами 5 и 1 = 5 ед.²
Опустим высоту с стороны прямоугольника длиной 1 ед. Она будет равняться 2, так как высота будет параллельна с высотой слева. У нас получился ещё один прямоугольник с сторонами 5 и 2. Его площадь равна 10 ед.² (если что, для площади прямоугольника мы умножаем стороны)
У нас также появился треугольник с сторонами 2 и (9-5) = 4. Найдём площадь данного треугольника: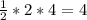 ед.²
ед.²
Треугольник слева будет равен треугольнику, который мы создали, так что его площади тоже равна 4 ед.²
Прибавляем все значения. Это равняется 23 ед.²
В трапеции ABCD угол A равен 90, градусов, боковая сторона CD перпендикулярна диагонали AC; CD равен 3 см, AD равен 5 см, 1) Найти площадь трапеции. 2) Найти площадь треугольника AMD, если M – середина CD.
1) АВ⊥АD, ВС║AD ⇒ ∠В=90°
СН - высота (ABCD)
Площадь трапеции равна произведению её высоты на полусумму оснований.
S(ABCD)=CH•(BC+AD):2
CH=AC•CD:AD
AC=√(AD²-CD²)=√(5²-3²)=4
CH=3•4:5=2,4 (см)
BC=AH=√(AC²-CH²)=√(16-5,76)=3,2
S(ABCD)=2,4•(3,2+5):2=9,84 см²
* * *
2) Найти площадь треугольника AMD, если M – середина CD.
СМ=MD ⇒АМ - медиана и делит площадь ∆ АСD пополам (свойство).
S AMD=[AC•CD:2]:2=4•3:4=3 см²
Объяснение: