Пусть AC=x, тогда в ΔABC по формуле Герона:
Решим квадратное уравнение относительно x².
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
По формуле связи косинуса и тангенса:
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK= > 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.
Sосн=√3 см²
α=30°
найти
SA,SB,SC,
Sб.п - ?
на основании пирамиды SABC правильный равносторонний треугольник ABC. AB=BC=AC=a
формула площади р.т
Sосн =а² ×√3 /4 отсюда сторона треугольника
а=√Sосн×4/√3=√ (4×√3)/√3=√4=2см
грань SAB наклонена к основанию ABC под углом,
двухгранный угол α=30°
находим высоту треугольника ABC на основании
H=CD=а×√3/2=2×√3/2=√3 см
высота треугольника SAB
SD=CD/cosα=√3/cos30°=√3÷√3/2=√3×2/√3=2см
высота пирамиды
SC=SD×sinα=2×sin(30°)=2×1/2=1 cм
длины рёбер SA=SB
SA=√BC²+SC²=√2²+1²=√4+1=√5 см
площадь грани SAB
S1=1/2×AB×SD=1/2×2×2=2см²
площадь грани SBC
S2=1/2×BC×SC=1/2×2×1=1 см²
грани SBC и SAC равны
площадь боковой поверхности пирамиды SABC,
Sб.п= S1+2×S2=2+2×1=4 см²
Пусть AC=x, тогда в ΔABC по формуле Герона:
Решим квадратное уравнение относительно x².
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
По формуле связи косинуса и тангенса:
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
В ΔABC по теореме косинусов:
По формуле связи косинуса и тангенса:
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
P(KLMN)=2a+2b=59
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK=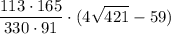 > 113/√421.
> 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.
Sосн=√3 см²
α=30°
найти
SA,SB,SC,
Sб.п - ?
на основании пирамиды SABC правильный равносторонний треугольник ABC. AB=BC=AC=a
формула площади р.т
Sосн =а² ×√3 /4 отсюда сторона треугольника
а=√Sосн×4/√3=√ (4×√3)/√3=√4=2см
грань SAB наклонена к основанию ABC под углом,
двухгранный угол α=30°
находим высоту треугольника ABC на основании
H=CD=а×√3/2=2×√3/2=√3 см
высота треугольника SAB
SD=CD/cosα=√3/cos30°=√3÷√3/2=√3×2/√3=2см
высота пирамиды
SC=SD×sinα=2×sin(30°)=2×1/2=1 cм
длины рёбер SA=SB
SA=√BC²+SC²=√2²+1²=√4+1=√5 см
площадь грани SAB
S1=1/2×AB×SD=1/2×2×2=2см²
площадь грани SBC
S2=1/2×BC×SC=1/2×2×1=1 см²
грани SBC и SAC равны
площадь боковой поверхности пирамиды SABC,
Sб.п= S1+2×S2=2+2×1=4 см²