x - 3y - 4z + 17 = 0
Объяснение:
Общее уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C, D - числа. В данном случае A = 1, B = -3, C = -4, D = -71.
Упрощенно говоря, параллельные плоскости отличаются коэффициентом D в уравнении.
Найдем D по формуле , где - координаты точки, через которую проходит нужная нам плоскость.
D = - (1*1 -3*2 -4*3) = - (1 - 6 - 12) = - (-17) = 17
Получаем уравнение плоскости, параллельной данной: x - 3y - 4z + 17 = 0
x - 3y - 4z + 17 = 0
Объяснение:
Общее уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C, D - числа. В данном случае A = 1, B = -3, C = -4, D = -71.
Упрощенно говоря, параллельные плоскости отличаются коэффициентом D в уравнении.
Найдем D по формуле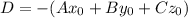 , где
, где 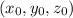 - координаты точки, через которую проходит нужная нам плоскость.
- координаты точки, через которую проходит нужная нам плоскость.
D = - (1*1 -3*2 -4*3) = - (1 - 6 - 12) = - (-17) = 17
Получаем уравнение плоскости, параллельной данной: x - 3y - 4z + 17 = 0