Даны вершины треугольника A(−2,1), B(3,3), С(1,0). Найти:
а) длина стороны AB = √((3-(-2))² + (3-1)² = √(25 + 4) = √29.
б) уравнение медианы BM.
Находим координаты точки М как середины стороны АС.
М(((-2+1)/2; (1+3)/2) = (-0,5; 2).
Вектор ВМ = ((-0,5-3); (2-3)) = (-3,5; -1).
Уравнение ВМ: (х – 3)/(-3,5) = (у – 3)/(-1). Это в каноническом виде.
Оно же в общем виде 7у – 2х – 15 = 0.
И в виде уравнения с угловым коэффициентом у = (2/7)х + (15/7).
в) cos угла BCA.
Вектор СВ = ((1-3); (0-3)) = (-2; -3). Модуль равен √(4 + 9) = √13.
Вектор СА = ((1-(-2)); (0-1)) = (3; -1). Модуль равен √(9 + 1) = √10.
cos(BCA) = (-2*3 + (-3)*(-1))/( √13*√10) = -3/√130 ≈ -0,26312.
г) уравнение высоты CD.
Находим уравнение стороны АВ.
Вектор AB = ((3-(-2)); (3-1)) = (5; 2).
Уравнение АВ: (х + 2)/5 = (у -1)/2 или у = (2/5)х + (9/5).
Угловой коэффициент перпендикуляра к АВ (это высота СD) равен -1/(2/5) = -5/2. Подставим координаты точки С.
0 = (-5/2)*1 + b. Отсюда b = 5/2.
Уравнение CD: y = (-5/2)x + (5/2).
д) длина высоты СD.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = (A·Mx + B·My + C)/√A2 + B2
Подставим в формулу данные: координаты точки С(1; 0) и уравнение прямой АВ:
2х – 5у + 9 = 0.
d = (2·1 + (-5)·0 + 9)/√22 + (-5)2 = (2 + 0 + 9)/√4 + 25 =
= 11/√29 = 11√29/29 ≈ 2.0426487.
е) площадь треугольника АВС по векторам.
Если вершины треугольника заданы, как точки в прямоугольной декартовой системе координат: A1(x1,y1), A2(x2,y2), A3(x3,y3), то площадь такого треугольника можно вычислить по формуле определителя второго порядка:
S= ± (1 /2) *(x1−x3 y1−y3 )
(x2−x3 y2−y3 )
x1−x3 y1−y3
x2−x3 y2−y3
A(−2,1), B(3,3), С(1,0).
S = (1/2)}|((-2-1)*(3-0) – (1-0)*3-1))| = (1/2)*|(-9-2)| = 11/2 = 5,5 кв.ед.
Даны вершины А(3; -1), B(2; 2), C(4; 1).
Вектор АВ: (-1; 3), вектор АС: (1; 2).
Уравнение прямой АВ: (х - 3)/(-1) = (у + 1)/3,
Общее уравнение АВ: 3х + у - 8 = 0.
Уравнение прямой АС: (х - 3)/(1) = (у + 1)2,
Общее уравнение АС: 2х - у - 7 = 0.
Точки на биссектрисе угла А равно удалены от сторон АВ и АС.
Используем формулу расстояния точки от прямой и приравняем расстояние до АВ и АС.
d=|Ax0+By0+C|/√(A²+B²).
Пусть точка на биссектрисе имеет координаты (х; у).
Находим значения √(A²+B²) для прямых АВ и АС.
Для АВ: √(3²+ 1²) = √10, для АС: √(2²+ (-1)²) = √5.
Получаем:
Раскроем модули. Для внутреннего угла А подходит уравнение с минусом:
Домножим числитель и знаменатель правой дроби на корень из 2 и приравняем числители.
Отсюда получаем ответ.
Уравнение биссектрисы угла А имеет вид:
х(3 + 2√2) + у(1 - √2) - (8 + 7√2) = 0.
Можно дать в цифровом виде: общее уравнение
Х - 0,071067812 У - 3,071067812 = 0 или с угловым коэффициентом: у = 14,07106781 х - 43,21320344 .
Даны вершины треугольника A(−2,1), B(3,3), С(1,0). Найти:
а) длина стороны AB = √((3-(-2))² + (3-1)² = √(25 + 4) = √29.
б) уравнение медианы BM.
Находим координаты точки М как середины стороны АС.
М(((-2+1)/2; (1+3)/2) = (-0,5; 2).
Вектор ВМ = ((-0,5-3); (2-3)) = (-3,5; -1).
Уравнение ВМ: (х – 3)/(-3,5) = (у – 3)/(-1). Это в каноническом виде.
Оно же в общем виде 7у – 2х – 15 = 0.
И в виде уравнения с угловым коэффициентом у = (2/7)х + (15/7).
в) cos угла BCA.
Вектор СВ = ((1-3); (0-3)) = (-2; -3). Модуль равен √(4 + 9) = √13.
Вектор СА = ((1-(-2)); (0-1)) = (3; -1). Модуль равен √(9 + 1) = √10.
cos(BCA) = (-2*3 + (-3)*(-1))/( √13*√10) = -3/√130 ≈ -0,26312.
г) уравнение высоты CD.
Находим уравнение стороны АВ.
Вектор AB = ((3-(-2)); (3-1)) = (5; 2).
Уравнение АВ: (х + 2)/5 = (у -1)/2 или у = (2/5)х + (9/5).
Угловой коэффициент перпендикуляра к АВ (это высота СD) равен -1/(2/5) = -5/2. Подставим координаты точки С.
0 = (-5/2)*1 + b. Отсюда b = 5/2.
Уравнение CD: y = (-5/2)x + (5/2).
д) длина высоты СD.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = (A·Mx + B·My + C)/√A2 + B2
Подставим в формулу данные: координаты точки С(1; 0) и уравнение прямой АВ:
2х – 5у + 9 = 0.
d = (2·1 + (-5)·0 + 9)/√22 + (-5)2 = (2 + 0 + 9)/√4 + 25 =
= 11/√29 = 11√29/29 ≈ 2.0426487.
е) площадь треугольника АВС по векторам.
Если вершины треугольника заданы, как точки в прямоугольной декартовой системе координат: A1(x1,y1), A2(x2,y2), A3(x3,y3), то площадь такого треугольника можно вычислить по формуле определителя второго порядка:
S= ± (1 /2) *(x1−x3 y1−y3 )
(x2−x3 y2−y3 )
x1−x3 y1−y3
x2−x3 y2−y3
A(−2,1), B(3,3), С(1,0).
S = (1/2)}|((-2-1)*(3-0) – (1-0)*3-1))| = (1/2)*|(-9-2)| = 11/2 = 5,5 кв.ед.
Даны вершины А(3; -1), B(2; 2), C(4; 1).
Вектор АВ: (-1; 3), вектор АС: (1; 2).
Уравнение прямой АВ: (х - 3)/(-1) = (у + 1)/3,
Общее уравнение АВ: 3х + у - 8 = 0.
Уравнение прямой АС: (х - 3)/(1) = (у + 1)2,
Общее уравнение АС: 2х - у - 7 = 0.
Точки на биссектрисе угла А равно удалены от сторон АВ и АС.
Используем формулу расстояния точки от прямой и приравняем расстояние до АВ и АС.
d=|Ax0+By0+C|/√(A²+B²).
Пусть точка на биссектрисе имеет координаты (х; у).
Находим значения √(A²+B²) для прямых АВ и АС.
Для АВ: √(3²+ 1²) = √10, для АС: √(2²+ (-1)²) = √5.
Получаем: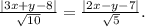
Раскроем модули. Для внутреннего угла А подходит уравнение с минусом: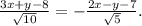
Домножим числитель и знаменатель правой дроби на корень из 2 и приравняем числители.
Отсюда получаем ответ.
Уравнение биссектрисы угла А имеет вид:
х(3 + 2√2) + у(1 - √2) - (8 + 7√2) = 0.
Можно дать в цифровом виде: общее уравнение
Х - 0,071067812 У - 3,071067812 = 0 или с угловым коэффициентом: у = 14,07106781 х - 43,21320344 .