Пусть дана равнобедренная трапеция с диагоналями см и см — медиана (см. вложение).
Сделаем дополнительное построение: проведем прямую . Образовался равнобедренный треугольник с боковыми сторонами см, равновеликий с трапецией (так как треугольники и равны по третьему признаку равенства треугольников). Следовательно, средние линии и тоже равны (средние линии и соответственно равны треугольникам и ).
Рассмотрим равнобедренный треугольник . Так как см — его средняя линия, то см. Опустим перпендикуляр — высота, биссектриса и медиана. Значит, см.
Рассмотрим прямоугольный треугольник
По теореме Пифагора: см.
Следовательно, площадь треугольника составляет см².
Так как треугольник и трапеция равновеликие, то площадь трапеции равна 48 см².
Пусть дана равнобедренная трапеция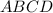 с диагоналями
с диагоналями 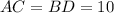 см и
см и 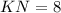 см — медиана (см. вложение).
см — медиана (см. вложение).
Сделаем дополнительное построение: проведем прямую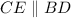 . Образовался равнобедренный треугольник
. Образовался равнобедренный треугольник 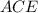 с боковыми сторонами
с боковыми сторонами 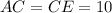 см, равновеликий с трапецией
см, равновеликий с трапецией 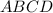 (так как треугольники
(так как треугольники 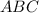 и
и 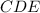 равны по третьему признаку равенства треугольников). Следовательно, средние линии
равны по третьему признаку равенства треугольников). Следовательно, средние линии 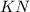 и
и 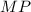 тоже равны (средние линии
тоже равны (средние линии 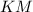 и
и 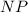 соответственно равны треугольникам
соответственно равны треугольникам 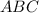 и
и 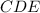 ).
).
Рассмотрим равнобедренный треугольник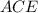 . Так как
. Так как 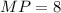 см — его средняя линия, то
см — его средняя линия, то 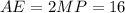 см. Опустим перпендикуляр
см. Опустим перпендикуляр 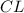 — высота, биссектриса и медиана. Значит,
— высота, биссектриса и медиана. Значит, 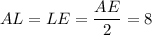 см.
см.
Рассмотрим прямоугольный треугольник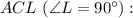
По теореме Пифагора: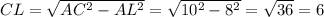 см.
см.
Следовательно, площадь треугольника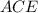 составляет
составляет 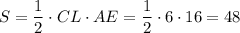 см².
см².
Так как треугольник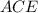 и трапеция
и трапеция 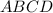 равновеликие, то площадь трапеции равна 48 см².
равновеликие, то площадь трапеции равна 48 см².
ответ: 48 см².