По формуле Герона найдем площадь одного из треугольников, на которые разбивается параллелограмм его диагональю
S=
p=(13+14+15):2= 21см
S= см^2
Но с другой стороны S=a*h
84=14*h, h= 6 см
По теореме косинусов найдем угол при основании параллелограмма
2ab*cosα = a²+b²-d²
2*13*14*cosα = 13²+14²-15²
cosα = (169+196-225)/364 = 140/364 = 5/13
sinα = √1-cos²α = √(13²-5²)/13² = 12/13
Высота h = a*sinα = 13*12/13 = 12 cм
ответ: наименьшая высота параллелограмма 12 см
PS В предыдущем решении S - площадь тр-ка, а не параллелограмма
По формуле Герона найдем площадь одного из треугольников, на которые разбивается параллелограмм его диагональю
S=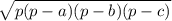
p=(13+14+15):2= 21см
S=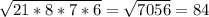 см^2
см^2
Но с другой стороны S=a*h
84=14*h, h= 6 см
По теореме косинусов найдем угол при основании параллелограмма
2ab*cosα = a²+b²-d²
2*13*14*cosα = 13²+14²-15²
cosα = (169+196-225)/364 = 140/364 = 5/13
sinα = √1-cos²α = √(13²-5²)/13² = 12/13
Высота h = a*sinα = 13*12/13 = 12 cм
ответ: наименьшая высота параллелограмма 12 см
PS В предыдущем решении S - площадь тр-ка, а не параллелограмма